2018-04-18

角度データの変化検知を可視化するプロット

解析

概要

角度データの解析を勉強しています。

角度データのモデリング (ISMシリーズ:進化する統計数理)

作者: 清水邦夫
出版社/メーカー: 近代科学社
発売日: 2018/01/30
メディア: 単行本
この商品を含むブログを見る

この書籍中ではP95で、時系列角度データの変化点の検出について1節割かれています。しかし実際に可視化した際にどのような挙動を示すのか図表がなく分からなかったので、可視化してみました。

データの生成

いつも通りjupyterで実験しました。簡単にvon mises分布を2つ容易して、それを結合します。以下の例ですと系列店700の段階で傾向が変わったということですね。可視化した際にもなんとなくわかりますが、von mises分布自体のノイズが大きいので判断が難しいです。

import matplotlib.pyplot as plt
from scipy.stats import vonmises
%matplotlib inline

fig = plt.figure()
ax = fig.add_subplot(1,1,1)
I = 1000
i1 = 700
i2 = 300
x = np.arange(0, I)
y1 = vonmises.rvs(kappa=0.8, loc=0, size=i1)
y2 = vonmises.rvs(kappa=0.4, loc=np.pi/2, size=i2)
y = np.concatenate([y1, y2])
ax.plot(x, y)

f:id:ajhjhaf:20180418201352p:plain

累積和プロット(Cumulative sum plot; CUSUM plot)

CUMSUMプロットでは、生成された角度を正弦と余弦に分解した時に、それぞれの成分の累積値をプロットします。同じ分布から生成された角度の累積値は一定の傾向を持ち続けますが、分布が変化した時にこの傾向が変わる、といった点から判断できるようです実際にノイズが取り除かれて、可視化結果も分かりやすくなっています。

fc = np.vectorize(lambda x: np.cos(x / 2 / np.pi))
cosy = fc(y)
c = np.cumsum(cosy)

fs = np.vectorize(lambda x: np.sin(x / 2 / np.pi))
siny = fs(y)
s = np.cumsum(siny)

fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(c, s)
ax.set_xlabel("Cumulative cosine value")
ax.set_ylabel("Cumulative sine value")

f:id:ajhjhaf:20180418201929p:plain

累積平均方向プロット(cumulative mean directional plot)

このプロットでは、系列における時点jまでの累積平均方向をプロットします。分布が変化すると、平均の方向も変化するのでやはり判定できるといったものです。テキストではcos, sinの累積成分 $C_j$ , $S_j$ とそこから求められる合成ベクトルの長さ $R_j$ に対して

$\cos{\bar{\theta_j}} = \frac{C_j}{R_j}$

あるいは

$\sin{\bar{\theta_j}} = \frac{S_j}{R_j}$

を満たす $\theta_j$ をプロットすると書いてあります。ですが、これを求める際には

$\tan{\bar{\theta_j}} = \frac{\sin{\bar{\theta_j}}}{\cos{\bar{\theta_j}}} = \frac{\frac{S_j}{R}}{\frac{C_j}{R}} = \frac{S_j}{C_j}$

なので、別に $R_j$ は必要ありません。また系列の最初の方ではnが少なくて値が安定しません。なので、最初100を削ってスケールを合わせたものも出してみました。

y_bar = np.arctan(s/c)

fig = plt.figure()

ax = fig.add_subplot(2,1,1)
ax.plot(x, y_bar)
ax.set_xlabel("series")
ax.set_ylabel("average direction")

ax = fig.add_subplot(2,1,2)
ax.plot(x[100:], y_bar[100:])
ax.set_xlabel("series")
ax.set_ylabel("average direction")
ax.set_xlim(0, I)

f:id:ajhjhaf:20180418202829p:plain

ランク累積和プロット(rank CUSUM plot)

ランク化して計算します。今回扱うプロットの中では一番分かりやすいですね。元々の分布がなんだったかにも影響しそうですが、計算が面倒くさいだけあっていい感じです。

from scipy.stats import rankdata
gamma = 2 * np.pi * rankdata(y) / y.size
U = np.sqrt(2 / y.size) * np.cumsum(np.cos(gamma))
V = np.sqrt(2 / y.size) * np.cumsum(np.sin(gamma))
B = np.sqrt(np.power(U, 2) + np.power(V, 2))

fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(x / I, B)
ax.set_xlabel("relative series")
ax.set_ylabel("B")

f:id:ajhjhaf:20180418203106p:plain

累積円周分散プロット(cumulative circular variance plot)

テキスト中では

各j=1,...,nに対して、円周分散1-R_jを計算し…

と書いてありますが、正しくは合成ベクトルの大きさ $R_j$ ではなく、平均合成ベクトル長 $\bar{R_j}$ を使って計算する必要があります。傾向が累積平均方向ベクトルと変わらないですね。

r = np.sqrt(np.power(c, 2) + np.power(s, 2))
r_bar = r / np.arange(1, I+1)
v = 1 - r_bar

fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(x, v)
ax.set_xlabel("series")
ax.set_ylabel("cumulative circular variance")

f:id:ajhjhaf:20180418203433p:plain

まとめ

可視化を駆使することで、時系列で得られた角度データの変化を分析することが出来ました。分析に役立てていきましょう。

2018-02-12

Python + Pyomoによる(非線形)数値最適化

最適化モデリング

TL; DR

Pythonのデータマネジメント技術と数値最適化をスムーズに繋げたい
Pyomoを使うことで自然な記法でモデルを組み立てることが出来る
Webドキュメントは貧弱だが、コミュニティは活発!

概要

数値最適化は機械学習や数値モデリングの基礎も基礎ですが、単に役に立ちます。Pythonという観点を度外視すれば、いろいろな手段がありますが、基本的には共通するフローがあります。

現象から最適化したい目的関数を決定する
目的関数に付随する制約条件を立式化する
データを用意し、モデリング言語を記述する
モデルをソルバーへ投入し、解を得る

こういった作業をするための環境は商用でも色々と売られていまして、例えばAIMMS社とか、GAMS社、AMPL社といった会社は最適化の開発環境や言語を作って販売しています。

もちろん非商用でも、こういう団体は存在し、COIN-ORではライブラリやソルバーを開発して公開しています。商用のソフトウェアに比べれば少々パフォーマンスに劣りますが無料で使えるということを考えれば文句も出ません。

しかしながら、例えばAMPL言語の書き方を見てみると…ちょっとめんどくさそうです。Stanかよ。新しく言語を覚えるのは大体の場合面倒くさいので、実務でちゃちゃっと最適化したい場合には向きません。どうせだったらPythonで済ませられたらうれしいです。

Pythonで最適化？

Pythonで最適化する方法も色々あります。

Scipy.optimize

一番最初に思いつく方法だと思います。アルゴリズムも色々ありますし、導入も簡単です。ただし、簡単な最小化とか線形計画法(LP)に特化しています。もうちょっと痒いところに手が伸びるものが欲しいのです。

PuLP

日本語で調べるとこのライブラリについての記事が一番多く出てきます。PuLPは先程のCOIN-ORによって開発が進められているライブラリです。使いやすいですし、Sphinxでのドキュメントも有るのが個人的にはありがたいところです。

ただし自分が使う上では、

使えるソルバーが少ない
最近開発が停滞気味

といった2点が気になりました。

リポジトリに書いてあるように、PuLPはLP/MILP用ライブラリです。デフォルトソルバーはCOIN-OR CBCで、他に使えるのもCPLEX、GLPKなどLPソルバーです。非線形問題は解けません。

もう一つ、PuLPは2017年の中頃からレポジトリが更新されていません。ドキュメントも更新がされておらず、実際に使う上で良く分からないことも多いです。というか英語ドキュメントすらなさすぎて、日本語記事のほうが詳しいかも…。先行記事では

などがありました。他にもQiitaやBlog上に、沢山の詳しい記事があります。

CVXPY

こちらの記事がとても詳しいです*1。

myenigma.hatenablog.com

PyomoはOpen-OR のウェブページにも載っていますが、メインで開発しているのは米サンディア国立研究所のようです。昔はCooprという名前でした。Pythonのオブジェクト指向な書き方をとても重視したライブラリです。しかし僕はPuLPの次にこれを使ってみたら、結構似ていると感じたので、移行も簡単でしょう。PyomoやPuLPは2008年ぐらいに沢山開発されたPythonライブラリで、今も生き残っているものたちです。なので、書きやすさは担保されていると思います(参考↓)。

Pyomoの嬉しいところは他に2つあって、

使えるソルバーが多い
コミュニティがそこそこ活発

という点です。PyomoはNLフォーマットを利用するソルバー(AMPL Solver Library)に対応しています。PuLPで使えていたCBC、GLPK、CPLEXなども利用することが出来ますし、その他についてはAMPLのページを見たほうが早いですね。PuLPでは使えなかった非線形ソルバーで有名なSCIPが使えますし、Open-OR主導で開発されているBonminやCouenne、IPOPTなども利用できます。ありがたいものです。

もう一つ、PyomoはPuLPと同じぐらいドキュメントは弱いのですが*2、コミュニティは活発です。リポジトリは頻繁にコミットがありますし、チュートリアル用のリポジトリやモデル例もあります。個人的に一番ありがたかったのは、Google Groupが活発で、質問にすぐに答えてくれた点です。

そういうわけで、今回はPyomoを使って最適化を試してみます。先行記事には

がありました。他に日本語の記事があまり出てこないので、残しておきます。

導入

ローカルへ構築

ライブラリ自体は

$ pip install pyomo

で終わりですが、これだとソルバーが全然入っていません。ソルバーはコマンドラインから実行できるようにする必要があります。自分はOSXの端末に以下のソルバーを入れました。皆様はお好きにどうぞ。

glpk
- brew install glpkで終了！
CPLEX
- アカデミックライセンスを使いました。
- IBMのインストーラーで導入後、/Applications/CPLEX_Studio128/cplex/bin/x86-64_osxへPATHを通せばOKです。
IPOPT
- こちらを参照しました。少し古い記事ですが、この通りで動きます*3。
SCIP
- そのまま導入しただけでは利用することが出来ません。
- Google Groupではnlオプションを付ければいいと書いてありましたが、僕は無理でした。
- SCIPをAMPLフォーマットで読み書きするようにコンパイルする必要があります。これはこちらをそのまま参考にしました。
Bonmin、Couenne
- Open-ORのソルバーなので、IPOPTと同様の手順で入ります。
- IPOPTの時にOPENBLASやLAPACKを入れていれば、飛ばしてOKです。

Dockerを利用する(2019-03-29追記)

Dockerを使ったコンテナを作りました。以下のページに詳細は書きましたので、面倒くさい方はこちらをどうぞ。

ajhjhaf.hatenablog.com

非線形 最適化問題を解く

どうせなので、非線形問題を解いてみましょう。例として、放送大学の資料にあった問題を解きます。

工数の最適配分の計算

* 工程i(i=1, 2, ..., n)にx_i(日)かけたときの仕上がりの程度がlog(a_i * x_i + 1) ただしa_i > 0 で決定する
*  各工程には最低でt_i(>0)日必要である
*  全行程をT日以内に終わらせる必要がある
*  仕上がりを最大化するには、各工程にどのように割り振ればいいか

仕上がりの程度にlogが入っているので非線形最適化問題になります。細かく言うなら、変数であるxが整数しか取らないので、整数非線形計画法(Integer Non Linear Programming; INLP)というパラダイムで解かれる問題ですね。ただし整数計画問題(Integer Programming; IP)やより狭義の整数線形計画問題(Integer Linear Programming)に特化した研究は色々ありますが、INLPに特化したものは少なく、一部の変数だけが整数条件を取る混合整数非線形計画法(Mixed INLP; MINLP)の一部として取り組むことが多いです。ソルバーもMINLP用のものを探したほうがいいです。

以下Jupyter + Pythonでの解法です。

2, 26行目: これはJupyter環境でやっています。Pyomoの例題ではコマンドラインから動かしていますが、こうすればJupyterでも動きます。optの部分でsolverを指定して下さい。
7, 9行目: PyomoはList型のIndexingを自動でやってくれないので、Dict型に変換しています。
14行目: 変数についてはVarで宣言し、2つめの位置変数へデータ型を入れます。今回は日数なので、非負整数です。
16~20行目: 制約条件を書いていきます。最適化条件と順番が前後しても大丈夫です。
- Pyomoの変な特性ですが、グローバル変数とローカル変数がごっちゃになっても受け付けてしまいます。より良い書き方がありそうですが…現状知りません。
21行目: 制約条件時に、Iの各要素iで成立…としたい場合は、第一位置変数へ入力すれば受け付けてくれます。
22~24行目: 最適化条件を書きます。senceで最大化(maximize) or 最小化(minimize)を指定します。
27行目: opt.solveをする時に、tee=Trueとすればソルバーのメッセージが表示されます。デバッグ時に便利です。
28行目: モデルの結果を表示します。

以下出力です(デバッグ部分は除きました)。

Model Days allocation

  Variables:
    x : Size=4, Index=I
        Key : Lower : Value : Upper : Fixed : Stale : Domain
          1 :     0 :  15.0 :  None : False : False : NonNegativeIntegers
          2 :     0 :  20.0 :  None : False : False : NonNegativeIntegers
          3 :     0 :  50.0 :  None : False : False : NonNegativeIntegers
          4 :     0 :  15.0 :  None : False : False : NonNegativeIntegers

  Objectives:
    value : Size=1, Index=None, Active=True
        Key  : Active : Value
        None :   True : 19.26358596079164

  Constraints:
    const1 : Size=1
        Key  : Lower : Body  : Upper
        None :  None : 100.0 : 100.0
    const2 : Size=4
        Key : Lower : Body : Upper
          1 :  15.0 : 15.0 :  None
          2 :  20.0 : 20.0 :  None
          3 :  50.0 : 50.0 :  None
          4 :   5.0 : 15.0 :  None

4つのタスクに対して、15:20:50:15と割り振ることでパフォーマンスが最大化され、パフォーマンス和は19.26です。さっさと終わる仕事の4番目ですが、プロトタイプが出来てからの伸びしろが良いのでこうなるわけです。

おわり

以上Pythonでの数値最適化でした。皆様も是非ガシガシ最適化して、ついでにブログもアップして、勉強させて下さい。

参考

統計数理研究所セミナー資料(伊藤聡先生)

*1:解説が薄いのは、このライブラリ(記事)を見つけたのが記事を書き終わってからというだけであり、他意はありません

*2:APIが纏められていない点が使いづらいです。出版されている本に載っているようですが、高い…

*3:昨年末に書かれた記事があったので、心配はしていませんでした

2018-02-03

Pythonによる超初歩的な金融資産解析(ついでのビットコイン)

解析

概要

資産を増やす金融商品として、投資信託や株、債権なんかがメジャーです。初歩的なポートフォリオ理論では

株などの資産がどのように変動するかは予測することが出来ない
一方で経済は成長するので、全体を長期的に見たらプラスに成長する
なので、分散して投資することで安定的な利益を得ることが出来る

といったことが前提とされます。即ち、価格の変動が正規分布に従ってランダムウォークするとみなして、観測された変動の平均と分散を元に、どれだけリスクを取ることが出来るかを踏まえて資産の内訳を作ります。そのため様々な株式や債権を纏めた商品である投資信託は、理論的には優等生な商品と見なすことができます*1。

正直な所、金融商品については、記載情報を見ても何を買うべきなのかよく分かりません。一方で、金融では時系列データが結構揃っていて弄ってみるだけでも面白そうです。今回はデータのハンドリングを通して、初歩的な金融資産のバランシングについて解析しました。

注意

マサカリ歓迎です。特にこの記事の筆者は金融業界について全くの素人です。橘玲氏の本を読んだ程度の知識しかありません。
この記事によって生じたあらゆる事象について、筆者は責任を負いません。
この記事は個人の見解と趣味の産物であり、投資を勧めるものでは全くありません。ほんとに。

材料

投資信託基準価格

以下のものをそれぞれのWebサイトからダウンロードしました。

三井住友 - 三井住友・DCつみたてNISA・全海外株インデックスファンド: モーニングスターより
レオス－ひふみプラス: モーニングスターより
ニッセイ -ニッセイTOPIXインデックスファンド: モーニングスターより
ニッセイ－ニッセイ日経２２５インデックスファンド: モーニングスターより
三井住友･日本債券インデックス・ファンド: モーニングスターより
Vanguard total world stock(VT): Yahoo! Financeより
Vanguard total stock marcket ETF(VTI): Yahoo! Fiananceより
Vanguard FTSE Emerging Markets ETF(VWO): Yahoo! Fiananceより

つまり、国内系ファンドはモーニングスター、海外ETFはY! Financeです。国内ファンドはSBIで購入することが出来るものしかありませんから、そちらからもダウンロードできます。しかし自分の環境*2では、csvファイルなのに違う拡張子としてダウンロードされたり、ファイルフォーマットが分析に使いづらいものだったので利用をやめました。モーニングスターはWebサイトが重いという欠点はありますが、ヘッダーがすっきりしていて使いやすいです。

ファンドの選定基準としては、以下のとおりです。

SMBC全海外: 日本を除いた全世界ファンド
ひふみプラス: 高パフォーマンスのアクティブファンド
TOPIX: 日本株式のベンチマーク
日系225: 大型日本株式のベンチマーク & TOPIXとの比較
日本債権: 債権を入れることのリスクのヘッジ率を知りたかった
VT: 全世界株式分散投資ファンド
VTI: 米国株式投資ファンド
VWO: 新興国分散投資ファンド

為替価格

海外ETFについては、ドル価格を円価格に修正する必要があります。今回はマネースクウェア・ジャパンからダウンロードしました。より長期のデータソースを知っている人が居たら教えてくれると助かります…。

実際には為替手数料がこの価格に加わる気がしますが、明るくないので割愛しました。

手法

いつものごとくPythonでやります。先ずダウンロードしてきたcsvファイルを読み込んでデータフレームを作ります。Y!から持ってきたデータはいいのですが、モーニングスターのそれはheaderが日本語です。なので、事前にエクセルなんかで英語に書き換えておかないとpandasが怒ります。注意して下さい。

基本的に終値、あるいは調整後終値で計算します。

import pandas as pd
import numpy as np

# USD/JPY比
exchange = pd.read_csv("USDJPY.csv", index_col=0, parse_dates=True)
exchange = exchange[["close"]]

# 日本系投資信託
smbc_astock = pd.read_csv("smbc_astock.csv", index_col=0, parse_dates=True)
smbc_astock.columns = ["smbc_astock"]

hifumi = pd.read_csv("hifumi.csv", index_col=0, parse_dates=True)
hifumi.columns = ["hifumi"]

topix = pd.read_csv("topix.csv", index_col=0, parse_dates=True)
topix.columns = ["topix"]

nikkei = pd.read_csv("nikkei.csv", index_col=0, parse_dates=True)
nikkei.columns = ["nikkei"]

smbc_jcredit = pd.read_csv("smbc_jcredit.csv", index_col=0, parse_dates=True)
smbc_jcredit.columns = ["smbc_jcredit"]

# 海外ETF
# USDで売られているので、為替価格の調整をする
vti = pd.read_csv("VTI.csv", index_col=0, parse_dates=True)
vti = vti[["Adj Close"]]
vti.columns = ["vti"]
vti = pd.DataFrame(vti["vti"] * exchange["close"], columns = ["vti"])
vti = vti.dropna()

vt = pd.read_csv("VT.csv", index_col=0, parse_dates=True)
vt = vt[["Adj Close"]]
vt.columns = ["vt"]
vt = pd.DataFrame(vt["vt"] * exchange["close"], columns=["vt"])
vt = vt.dropna()

vwo = pd.read_csv("VWO.csv", index_col=0, parse_dates=True)
vwo = vwo[["Adj Close"]]
vwo.columns = ["vwo"]
vwo = pd.DataFrame(vwo["vwo"] * exchange["close"], columns=["vwo"])
vwo = vwo.dropna()

# 全部結合する
df = pd.DataFrame([])
df = df.join([
                smbc_astock,
                hifumi,
                topix,
                nikkei,
                smbc_jcredit,
                vti,
                vt,
                vwo,
    ], how="outer")

# 日付情報を初日分から生成       
date = pd.DataFrame(index=pd.date_range(start=df.index[0], end="2018-01-30", period=1))
df = df.join(date, how="outer")
# dataframe用のラベル
order = [
            "smbc_astock",
            "hifumi",
            "topix",
            "nikkei",
            "smbc_jcredit",
            "vti",
            "vt",
            "vwo"
]

df = df[order]

続いて収益率を計算していきます。収益率は購入時の価格と比較した際の、得られる利益のパーセント値です。たとえば100円で購入した資産が110円になったら収益率は10%ですね。

今回はX[年|日]後の収益率を計算し、更に過去Y[年|日]間の収益率から、収益率の統計値を算出します。XとYについては、短期の動きと長期の動きのどちらを見たいのかで、短期: (X=Y=90日)、長期: (X=365年, Y=365年)としました。

今回の計算は最初のデータが有る日から、全日程を計算対象としています。ただし土日祝祭日は証券取引所が開いていないため、NaNになります。とはいえpandasが統計値を計算する時には、これを自動で取り除いてくれます。各商品毎に収益率を計算しているのは、日本とアメリカでNaNになる部分が異なるからです。

統計値については平均、分散、そしてシャープレシオを計算します。シャープレシオは平均/分散で定義される統計値です。高いほど良い金融資産というようにみなされるんだとか。

import matplotlib.pyplot as plt

# 収益率の計算
diff = 90
for i, o in enumerate(order):
    ds = df[o].dropna()
    rds = (ds.iloc[diff:].reset_index(drop=True) - ds.iloc[:-diff].reset_index(drop=True)) / ds.iloc[:-diff].reset_index(drop=True) * 100
    rds.index = ds.index[diff:]
    rdf = pd.DataFrame(rds)
    if i == 0:
        r = rdf
    else:
        r = r.join(rdf, how="outer")
r = r.join(date)


# 統計値の計算
ave_return_list = []
std_return_list = []
sharpe_ratio_list = []
term = 90
for i in range(len(r) - term):
    ave_return_list.append(r.iloc[i:term+i].mean())
    std_return_list.append(r.iloc[i:term+i].std())
    sharpe_ratio_list.append((r.iloc[i:term+i].mean() / r.iloc[i:term+i].std()).to_dict())
ave_return_df = pd.DataFrame(ave_return_list, index=r.index[term:])[order]
std_return_df = pd.DataFrame(std_return_list, index=r.index[term:])[order]
sharpe_ratio_df = pd.DataFrame(sharpe_ratio_list, index=r.index[term:])[order]

# 可視化
fig = plt.figure(figsize=(15,10))

ax = fig.add_subplot(3,2,1)
ave_return_df.plot(title="Long term",
                   xticks=[],
                   ax=ax,
                   legend=False)
ax.set_ylabel("Return")

ax = fig.add_subplot(3,2,2)
ave_return_df.plot(title="Short term",
                   xticks=[],
                   xlim=("2016-10-01", "2017-1-30"),
                   ylim=(-5,15),
                   ax=ax,
                   legend=False)

ax = fig.add_subplot(3,2,3)
std_return_df.plot(xticks=[],
                   ylim=(0,40),
                   ax=ax,
                   legend=False)
ax.set_ylabel("Risk")

ax = fig.add_subplot(3,2,4)
std_return_df.plot(xticks=[],
                   xlim=("2016-10-01", "2017-1-30"),
                   ylim=(0,10),
                   ax=ax,
                   legend=False)

ax = fig.add_subplot(3,2,5)
sharpe_ratio_df.plot(ax=ax,
                     ylim=(-5,20),
                     legend=False)
ax.set_ylabel("Sharpe ratio")

ax = fig.add_subplot(3,2,6)
sharpe_ratio_df.plot(xlim=("2016-10-01", "2017-1-30"),
                     ylim=(0, 4),
                     ax=ax,
                     legend=True)

ax.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)

plt.show()

最後に、計算した収益率からリスクリターン分布のプロットをします。この図は、横軸に収益率の分散、縦軸に収益率の平均をとったものです。詳細はWikipediaを見てもらうとして、今回挙げた金融商品を一定の割合で保持していた場合に、過去365日間での収益はいかほどだったのかを調べます。

金融資産の割合は、ディリクレ分布からパラメータを適当に変えて生成してみます。最終的に、シャープレシオの順にソートし、1年前に買っていたら今頃儲かっていたという、金融資産の割合を調べます。乱数から統計値を計算する際に、高速化のために逆ソートしてから計算しています。ソートせずに後ろからテーブルを出力しようとすると遅いです。

可視化は最終的に出力したテーブルから出しても良いのですが、そちらだと色が一色になって重なりが見えづらいです。

from scipy.stats import dirichlet
import matplotlib.pyplot as plt
%matplotlib inline

# 収益率の計算
diff = 365
for i, o in enumerate(order):
    ds = df[o].dropna()
    rds = (ds.iloc[diff:].reset_index(drop=True) - ds.iloc[:-diff].reset_index(drop=True)) / ds.iloc[:-diff].reset_index(drop=True) * 100
    rds.index = ds.index[diff:]
    rdf = pd.DataFrame(rds)
    if i == 0:
        r = rdf
    else:
        r = r.join(rdf, how="outer")
r = r.join(date)
[f:id:ajhjhaf:20180203000841p:plain]

# 資産割合の乱数を生成し、その度に可視化
fig = plt.figure(figsize=(15,5))
ax = fig.add_subplot(1,1,1)
result = []
term = 365
for alpha in [0.5, 5, 50, 500]:
    for i in range(2000):
        w = dirichlet.rvs(alpha=[alpha / df.shape[1]]*df.shape[1])[0]
        ave_r = r.sort_index(ascending=False).iloc[:term].mean()
        var_r = r.sort_index(ascending=False).iloc[:term].cov()
        e_ret = np.dot(w, ave_r)
        e_ris = np.sqrt(np.dot(np.dot(w, var_r), w.T))
        d = {"weight": w, "return": e_ret, "risk": e_ris, "ratio": e_ret / e_ris}
        result.append(d)
        ax.plot(e_ris, e_ret, "o", ms=3)
ax.set_xlabel("Risk(Standard deviation)")
ax.set_ylabel("Return(Average)")
ax.plot([0, 40], [0, 40])

# 集計
result_df = pd.DataFrame(result)
result_df = result_df.sort_values("ratio", ascending=False)
weight_df = (pd.DataFrame(result_df["weight"].values.tolist(), columns=order) * 100).round()
weight_df.index = result_df.index
result_weight_df = weight_df.join(result_df.sort_values("ratio", ascending=False)[["ratio", "return", "risk"]] / diff * 365)

結果

あまり大した考察は出来ませんが、コメントです。

90日での値動き

f:id:ajhjhaf:20180203063146p:plain

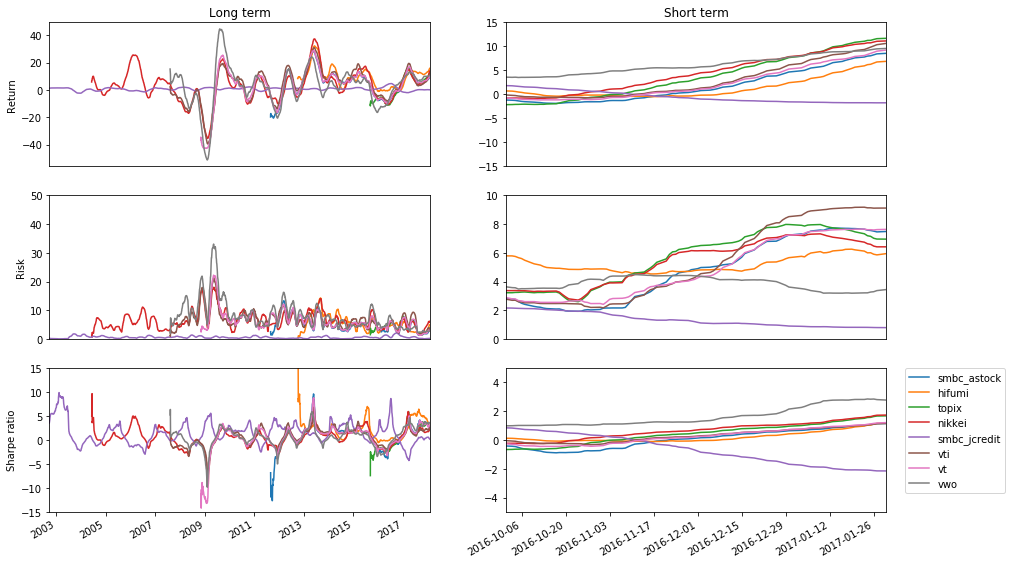
左側がx軸の時系列を長めに取った図、右側が最近の時系列に注目した図です。一番上の段が収益率平均、中段が収益率分散、下段がシャープレシオです。

収益率について、2008年ぐらいにリーマン・ショックがあって株価がめちゃめちゃに落ち込んでいます。しかしそこからは基本的に正のリターンを持っているので、儲かっていますね。ここ最近の収益率も右肩上がりです。
こういう図をプロットするまで信じていなかったのですが、たしかに債権はリーマン・ショックのときにも落ち込んでいませんし、資産担保が出来ています。まぁ、一方で全然プラスになっていませんが、安定的だということがわかります。2段目の分散も低いですね。
VTとSMBC 全海外は日本が含まれていないこと以外はポートフォリオが似ていますが、実際パフォーマンスも似ています。一方で、ここ最近は日本の株価が上昇傾向だったから、VTの方がパフォーマンスが良かったんですね。
VTIはVTよりパフォーマンスが良いと言われることもありますが、ここ最近は分散がかなり高いです。リターンも実際高いんですが、リスクの兼ね合いが大事です。
VWOの傾向から、ここ最近は新興国株が安定して上昇傾向だったことがわかります。リターンは高くとも、分散が低く、シャープレシオが凄いことになっていますね。

365日での値動き

f:id:ajhjhaf:20180203063209p:plain

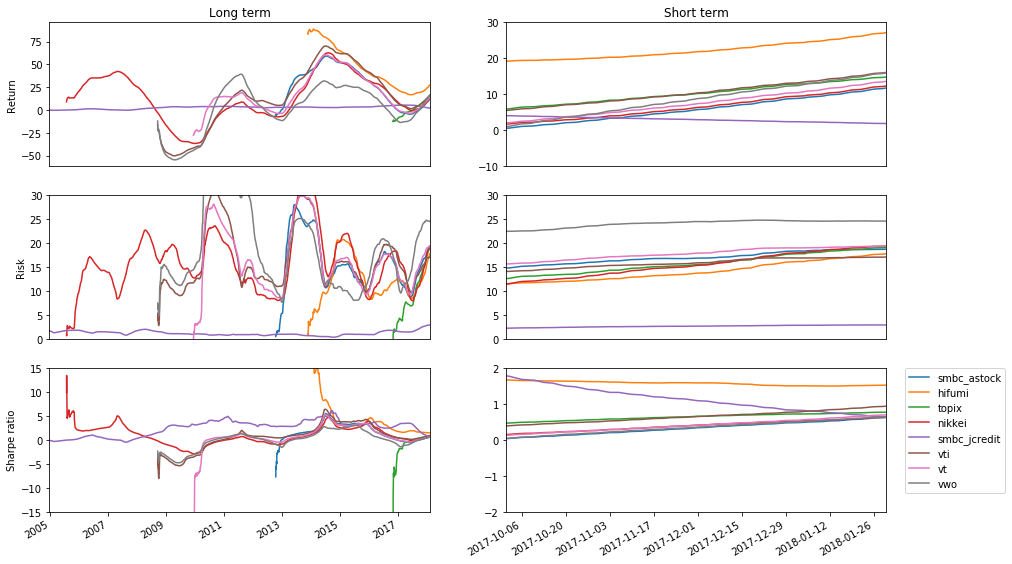
ひふみプラスが凄いことになっています。そりゃー人気が出るわけです。ただし、90日のプロットの方を見ればわかりますが、ここ最近のパフォーマンスはやや低めです。
90日の時には殆ど見られませんでしたが、365日だとファンドが始まった時にシャープレシオが安定しないように見えます。基本的に規模が小さすぎて、様子見状態で分散が小さいことが原因と推測します。
短期の場合と異なり、VWOの分散が最も高いです。ただしこちらのほうが、多く言われている状態に一致するようです。その分最近の新興国株式の状態が良かったと推測できます。
儲かっている時には資産がそちらに移動するようで、新興国株と日本債権のシャープレシオが見事に逆相関を描いています。

リスクリターン分布

f:id:ajhjhaf:20180203063240p:plain

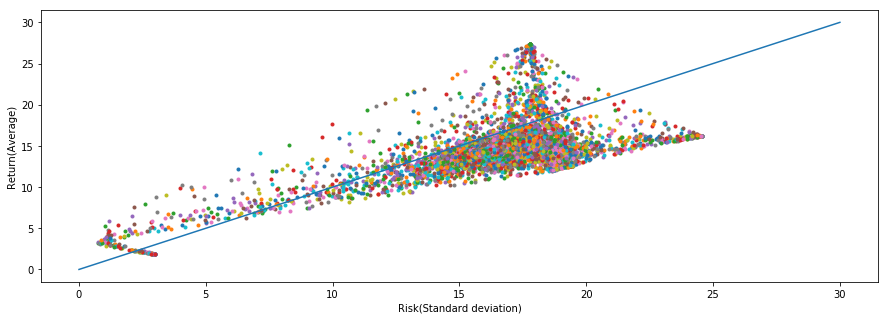
sharpe ratio順にソートしたものを上位10個だけ出力します。見やすくするために、1%以下の数値については丸めています。

index	smbc_astock	hifumi	topix	nikkei	smbc_jcredit	vti	vt	ratio	return	risk
1386	0	16	0	0	84	0	0	5.20125	5.88951	1.13233
313	0	12	0	3	84	0	0	5.09683	5.3542	1.0505
1108	0	12	1	0	83	0	4	4.97517	5.50391	1.10628
1103	0	6	0	7	86	0	0	4.95763	4.2625	0.859785
1302	0	11	0	0	87	1	1	4.95401	4.94603	0.998389
1495	0	4	0	8	86	0	2	4.93894	3.98458	0.806767
1470	0	12	0	0	88	0	0	4.50332	4.88915	1.08568
416	7	0	5	0	87	0	1	4.37415	3.30528	0.755639
1355	0	0	0	13	86	0	0	4.23473	3.36452	0.794506

効率的フロンティア曲線っぽいものが見えます。が、どこか歪な形ですね。今回は全部で8000個の乱数を生成しているんですが、出し方が完全にランダムなので効率があまり良くありません。シャープレシオが高くなるようにサンプリングを工夫すれば、もっとはっきりと見えるようになると思います。
表を単純に出力しただけでは、リスクをなんとか下げようとしてしまい、債権ばっかになってしまいます。これはこれで理想的なポートフォリオなんですが、リターンは大きくありません。試しにリターンが20%以上のバランスだけ見てみます。

index	hifumi	nikkei	smbc_jcredit	vti	vt	vwo	ratio	return	risk
1280	73	0	26	1	0	0	1.66061	20.6777	12.4519
1945	76	1	23	0	0	0	1.63506	21.3648	13.0667
217	75	0	24	0	0	1	1.63401	21.1787	12.9612
169	80	0	17	0	2	0	1.59045	22.6507	14.2417
176	87	0	12	1	0	0	1.58291	24.1981	15.2871
1440	84	0	14	0	0	2	1.5753	23.5152	14.9275
1246	87	1	12	1	0	0	1.57514	24.2402	15.3892
617	89	0	10	1	0	0	1.57479	24.7418	15.7112
1264	89	0	10	0	1	0	1.57079	24.71	15.7309

ひふみは面白いですね。インデックスファンドに勝利してるアクティブファンドって点で凄いと思いました。ただし、これが過去1年間の後ろ向き分析ということには注意して下さい。これから購入しても、同じパフォーマンスが得られるとは限りません。

このプロットには、自分のポートフォリオを載せることも出来ます。以下を乱数のプロットが終わった後に記述すればOKです。リバランスするときなんかに、役立てられると思います。

# 保有資産の割合を入力
w = np.array([0.5, 0, 0, 0, 0, 0.35, 0.15, 0])
expected_return = np.dot(w, ave_r)
expected_risk = np.sqrt(np.dot(np.dot(w, var_r), w.T))
sharpe_ratio = expected_return / expected_risk
print("{0}日の期待リターンは{1}%でした".format(diff, expected_return))
print("{0}日の期待リスクは{1}%でした".format(diff, expected_risk))
print("{0}日のシャープレシオは{1}%でした".format(diff, sharpe_ratio))
ax.plot(expected_risk, expected_return, "^", ms=20)

f:id:ajhjhaf:20180203063421p:plain

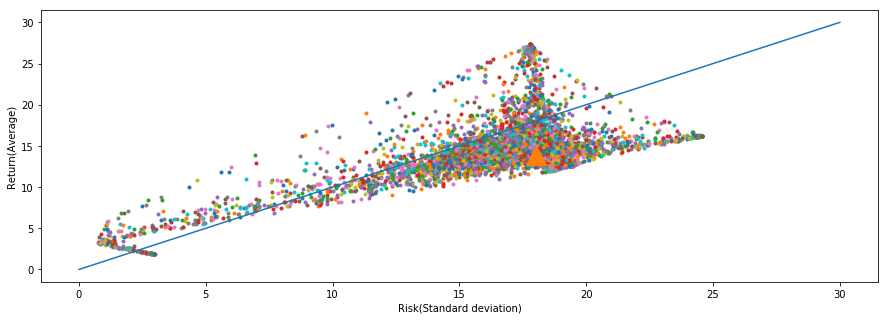
おまけ

ビットコインについての価格変動も、このスキームで調べてみましょう。今流行っているアレです。

ビットコイン価格

Yahoo! Financeからダウンロードしました。この価格はBTC-USDであることに注意してください。国内の投資信託と合わせるために、為替価格で補正する必要があります。

結果

ビットコインは値動きが激しいことが予測されるので、X=Y=30日での統計値を見ます。

f:id:ajhjhaf:20180203063834p:plain

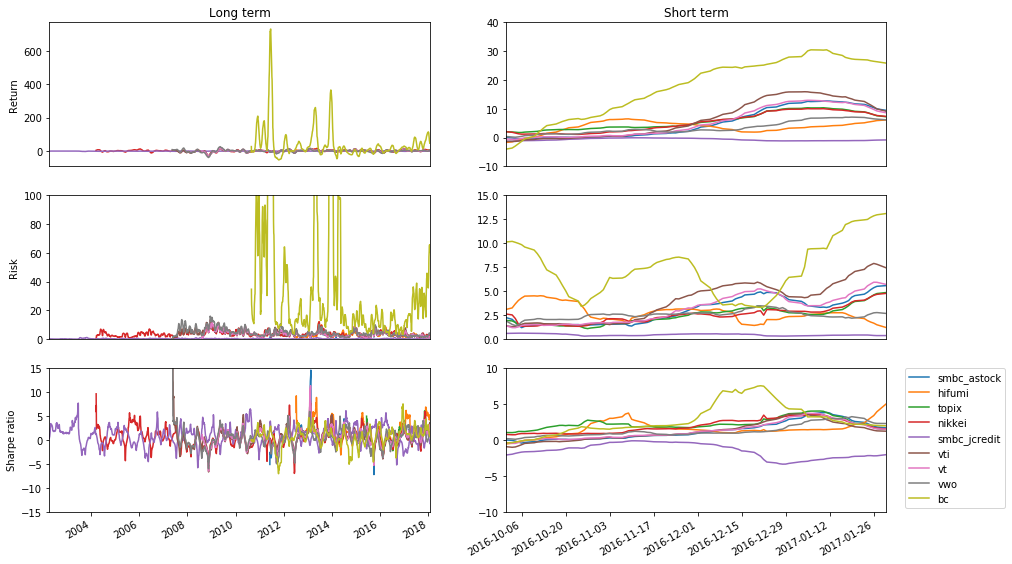
面白いことに、なんだかんだ言ってここ最近購入していても儲かる可能性はあったようです。ただし分散が30日間で平均してもずいぶん大きいです。なので購入するタイミング次第で物凄い高値を掴みうるリスクがあります。僕が友達と会って「最近ビットコインがアツいけど、もう手遅れだよね」と話したのが11月中頃でしたが、そういえば随分伸びたものです。しかしリスクが凄まじい。場合によっては資産が60%以上丸ごと減る可能性もあるわけです。

続いて直近の30日の履歴から求めたリスクリターン分布のプロットです。

f:id:ajhjhaf:20180203064100p:plain

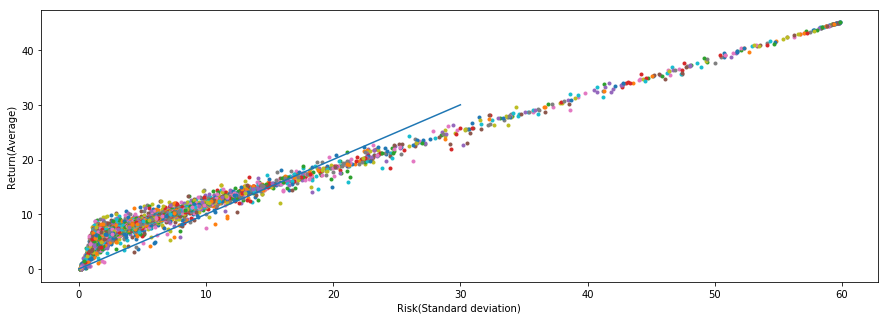
随分面白い形になりました。超ハイリターンハイリスク資産であるビットコインが入るとこんな感じになるんですね。この場合の最適ポートフォリオは次のとおりです。

index	smbc_astock	hifumi	topix	nikkei	smbc_jcredit	vti	vt	vwo	bc	ratio	return	risk
3856	2	43	0	1	29	0	2	20	2	87.9018	73.4374	10.1646
864	0	0	3	16	2	0	0	75	5	85.8413	94.9392	13.4562
2906	36	23	2	0	17	2	6	12	2	84.7379	68.2586	9.80057
3413	4	21	0	17	0	12	1	42	3	84.1403	90.7351	13.1203
2903	45	17	1	3	7	4	2	19	2	83.465	73.1678	10.6656
2375	52	21	0	3	5	2	0	14	2	83.228	75.7125	11.068
2958	4	52	8	0	8	0	10	15	2	82.6065	90.1786	13.2819
3859	6	15	0	1	1	15	14	45	3	82.3415	89.5655	13.2341
2399	7	0	2	1	6	0	0	79	5	81.6456	97.8794	14.5858

先程までのポートフォリオとは随分異なります。興味深いのはVWOの割合が高くなった点です。ビットコインも新興国株も投機的なところがありますので、この2つを持つことでリスクヘッジすることが出来るんでしょうか笑。仮想通貨界隈では、本格的に市場に出回る前のものをバラバラに買って、†神に祈る†といった投資方法があるようですが、このポートフォリオでもごく少量だけ保持することが示唆された点でも、それは結構合理的なのかもしれません。

とはいえ、仮想通貨での収入は雑収入扱いになるので、最大で50%の所得税がかかります。その点を考慮すると、また違った結果になりそうで面白いですね*3。

履歴

2018-02-02: 公開
2018-02-02: 信託報酬についてよくある勘違いをしていたのでコード、結果共に修正

*1:ただし、野村の解説にあるように、正規分布に従うランダムウォークは既に否定されています。そもそも変動が正規分布に従うなら、左右対称になっていつまでも経済が成長しません。なので個人的にも歪み正規分布と見なすほうが自然に思えます。「初歩的」と上述したのはそういうことです。

*2:Mac + Safari

*3:計算のどこに取り入れればいいのか分からない

2018-01-16

人生で初めて[海外に||一人で||猫と]暮らしている(現在進行系)

自己紹介

いい機会なので、滞在中の心境を研究留学 Advent Calendar 2017に似せたフォーマットで纏めておきます。

どうやって行ったか

8月11日、研究室の指導教員から「ベルギーにいる僕の友人が、短期滞在で研究員を探しているんですけど、興味ありますか？」と言われた。

自分が所属しているコースでは、課程を卒業するために日本国外で3ヶ月以上の研究留学、あるいはインターンシップに参加することが求められている。一方でこのコースに入っていると、特定の条件下で生活費が支給される。自分は元々留学には興味がなかったが、そちらの生活費が目当てで加入した。

ただ、その後別途生活費は確保することが出来たので、必ずしも海外に留学する必要は無くなった。何故ならこのコースは脱退罰則が定義されていない。所属することの恩恵は月々の収入や外部試験と出張の補助であるが、学振DC1を取っている場合これらの補助は殆ど自身で賄うことが出来る。なので留学が面倒ならば、課程自体を辞めてしまえばよい。

しかし海外で生活するということは自分にとっては全くの新体験。将来的に仕事でこういう機会は訪れるかもしれないが、Webを見ていると若いうちに海外での生活を経験しておくことは多くの収穫があると述べる文章は多い。

globalbiz.hatenablog.com

一方で、留学をすることで学位取得が遅れる可能性はある。しかしそのリスクを踏まえた上でも、長期的に見れば意味があるのかもしれないと考えて行くことを決めた。留学するならば、コースから補助が出るわけだし、経済的に損はない。そういうわけで、渡航費用*1と滞在費*2については負担が無い。ただしその他の生活費については自腹だった。

どこに行ったか (組織など)

ベルギーのKU Leuvenあるいは、VIBへ行った。滞在先のボスの正式な所属はVIB-KU Leuven Centerであり、自身のIDカードもKU Leuvenから発行されている。研究室もベルギー北部のLeuven市に存在する。しかし実質的な研究室ポジションはVIB寄りである。

VIB

VIB(Vlaams Instituut voor Biotechnologie)については邦語では殆ど情報がない。なお日本語の資料だと、東工大の調査レポートが分かりやすい。

VIBについて語るためには、まずベルギーについて語る必要がある。この国はチョコレート、小便小僧、国連本部というイメージで語られることが多い*3。実際にはヨーロッパ中でのポジショニングとしては複雑な国である。

九州程度の国土なのだが、その中でオランダ語圏、フランス語圏、そして少々のドイツ語圏が存在する。オランダ、イギリス、フランス、ドイツに囲まれるベルギーは古くからヨーロッパの交易の要所として栄えた。元々はオランダ語が優勢な国であったのだが、ナポレオンの統治の際にフランス語が公用語として使われた結果、国内のフランス語圏勢力が拡大する*4。一方で庶民の生活を描くことに重きをおいたロマン主義運動や、ポストナポレオンのパワーバランスの為に非フランスとしてのオランダが重視された結果オランダ語圏も力を持った。この結果としてフランス語圏とオランダ語圏が入り混じって存在するベルギーが生まれたのだとか。詳細は以下の新書を参考にして欲しい。

物語ベルギーの歴史 - ヨーロッパの十字路 (中公新書)

作者: 松尾秀哉
出版社/メーカー: 中央公論新社
発売日: 2014/08/22
メディア: 新書
この商品を含むブログ (10件) を見る

以上の経緯のために、国内では2つの勢力が独自に存在する。VIBはそのうち、オランダ語圏のフランデレン政府によって作られた生物学系の研究所だ。面白いのは、VIBそのものは研究所を保たないことである。フランデレン地方の大学と提携・資本協力することでそれぞれの大学に講座を構えている。この機関のもう一つの特徴は、産業創出を重視している点である。財源の少なくない割合を技術移転にあてており、実際に幾つかのベンチャー企業も誕生しているんだとか。VIBの年額の予算は2017年から5年かけて増額され5900万ユーロ程度(=80億円)まで引き上げられるらしい。これは大学の額と直接比較すると多くはない*5。注意するべきなのは、VIBはあくまで生命科学の研究所だと言う点だ。ここで比較するべきは全体額ではなくLife scienceの分野との比較であり、それだとMITでも1.29億ドル(=140億円)、大学平均だと68億円だ。しかもVIBの研究室は所属大学からの恩恵も受けられる。予算額としては中々良い研究機関である。

なぜそこへ行ったか

1番大きな理由はボスがその研究室のボスの元同僚だったからだ。知己があると行きやすい。ラッキー。

しかしもう1つ、滞在先のパフォーマンスに興味を持った。滞在先のボスは2017年度は30報の著者論文を書いた。この内インパクトファクターが10を上回る雑誌から出版されたものが12報あり、その内Natureへ3報、それとは別にNature系列へ3報出ている。個人的な感想を言えばモンスターだった。すごい。そのような環境で研究をすることで、パフォーマンスの秘密を知りたかった。

いつ行ったか

短期の滞在で、2017/12/01 ~ 2018/02/28まで滞在する予定で。ちょうど今日が折り返し地点というわけです。より具体的なスパンとしては、

6月: 滞在先のボスが来日し、カンファレンスで発表する。
8月: 声がかかる
9~10月: 日程調整
10月下旬: 日程決定
12月: 出発

といった流れだった。

このような日程になったのは3つの思惑が複雑に絡み合った結果と言えよう。

　1つ目は、自身の考えである。自分は滞在によって得られる経験値と、自身の研究が遅れるトレードオフを踏まえると、単位として最低限必要な3ヶ月がベストであった。特に後者の要因が非常に大きい。自分の所属している大学院の課程では、学位を取るために指導教員が著者に入っている(あるいは単著の)筆頭著者の査読付き論文と指導教員の合意が必要である*6。自分の場合だと、「指導教員が著者に入った」という点が重要である。この結果として、留学先に長期滞在して論文を発表したとしても、卒業要件の論文としてはカウントされない。そのため滞在すれば滞在するだけ、自身の研究は進まず卒業が難しくなる。

更に、自分の所属している大学院では、学位審査の委員会に指導教員が入っている。この制度は中々独特らしい。こちらの留学を妨げる要因となった。仮に読者がそこそこの貢献をした(指導教員も著者に入っている)論文を発表したとする。この場合でも指導教員の胸先一寸で学位取得が左右され、学位取得は安泰ではない。委員会に指導教員が入っているのだから、彼の人が持つ決定権が大きいのだ*7 *8。自分もリスクを考え、留学に来る前に日本の指導教員とこの点は話した*9。しかしながら彼の人曰く、「留学先で査読付き論文が出ても、それで学位をあげるつもりは無い」そうだ。以上の理由から、自分が長期的に滞在することは、学位取得の点ではまるで得が無い*10。よっていいとこ取り*11で3ヶ月を希望した。

2つ目は、滞在先のボスの思惑である。自分の研究領域はバイオインフォマティクスで基本的には生命科学 *12なので、3ヶ月では論文出版まで漕ぎ着けることが難しい。そのためより長期の滞在が期待され、国内のボスも混じえた日程調整に時間がかかって12月~2月の滞在となった。この日程だとビザを用意する必要もなく、色々と楽である。

3つ目は、予算機関の思惑である。自分の所属しているコースの予算は今年度末が期限だった。そのため、予算が満額支給されるためには、年度内に帰国する必要があった。

何をやっているか

当たり前だが守秘義務があるので、大した事は言えない。が、相変わらずバイオインフォマティクスをやっている。しかし元々自分は(これまでのブログ記事を見れば分かるように)統計学寄りで、塩基配列そのものはあまり触ってこなかった*13。今は塩基配列を触っており、BLASTやらSAMTOOLSやらSEQ-KITなどのツールを勉強する良い機会になった。

自分は外の釜の飯を食うことも重要だと思う。特定のテーマについて追求するためには、間違いなく継続的に続けることは重要だ。その点では留学は重荷でしか無い。一方で、特定のテーマについて掘り進める方法は色々ある。自分の研究室から離れて、異なるアプローチを知るためには武者修行が良い手段である。

何を知りつつ有るか

まだ現在進行系だが、色々と勉強になることが多い。依然わからないことも多い。

労働時間

よく言われることだが、こちらの人々は遅くまで働かない。大体17時ぐらいには帰り始め、18時ともなると殆どおらず、19時には研究室が真っ暗だ*14。予想はしていたが、長く労働する傾向の有る自分には衝撃的であった。とはいいつつも総労働時間が極端に短いわけでもない。朝来る時間はそこそこ早く、9時には結構な割合が来ているし、8時に来る人もいる。残業が無いと踏まえるのが適当だ。

滞在先のボスにこのことを訊いたが、結局帰ってからも仕事をしている人が多いらしいので、パフォーマンスの確実なミラクルは存在しないらしい。彼が述べていた興味深い仕事は、メンバーの忙しさを管理しているという事だ。仕事の中にも重い軽いはあるので、それを見極めて常に過負荷にならないように調整しているらしい。マネージャーともなれば当然なのかもしれないけれども、ラボのPIが単純に仕事を降るだけではなく、調整弁までこなしているのは安心することができよう。

ただまぁ、クリスマスはしっかりと休んでいた。自分の研究のメンターは12/20ぐらいから休暇を取り始め、1/5ぐらいまで現れなかった。研究所自体も12/23から1/1まで閉鎖された。

思うに彼らはメリハリの付け方が上手い。自分だと家に仕事を持ち帰りたくないので、研究室に滞在する時間が長くなりがちだ。スイッチングを調整できていることは、パフォーマンスの源泉の1つだろう。しかし、そのマインドの習得方法は未だにわからない。

ポジション

これもよく言われることだが、サポーティングスタッフが多い。所謂Lab technicianと呼ばれる。

Prof: 1
Post Dr. researcher: 5~6
Technician: 5~6
Doctor course student: 5~6
Master course student: 3~4?

ぐらいだろうか。これには秘書などの研究に関わらないメンバーは含めていない。更に学部生も居ない。そのため教育のためにかかるコストは日本と比べると低いように思える。

一方で、自分のイメージとは異なり、ポスドク研究者がチームをリードすることも多い。自分はこのような仕事は助教以上のタスクかと思っていたが、よりElderなポスドクには任されて責任著者へ繋げるらしい。とはいえ、これは研究室に依るのだろう。

VIBそれ自体でも、Techに対するサポートは篤い。VIBは様々なトレーニングコースを用意しており、自由に参加することも出来る。その中にはTechのみを対象としたものが数多く存在するし、キャリアについて考えるものが専用に用意されている。日本では研究をサポートするURA*15やTechが全然居らず、教員へ仕事が回ることでの負担が取り沙汰されるが、このような基盤まで固めるのは一朝一夕では無理だろう。

コミュニケーション

研究室のベルギー人率は50%程度で、内部の公用語は専ら英語だ。なので特に困ることはない。しかし行ってみるまで知らなかったのだが、研究室メンバーの女性の割合が非常に高い。男女比は3:7ぐらいだ。

そのためなのか、お昼ごはんを一緒に食べることが半ば1つの義務みたいになっている。この点は少しびっくりした。日本は集団文化であり、欧米は個人主義とは聞いたものだが、全く逆の状態であった。むしろ1人で食事をしていると心配されることが多い。少なくとも調べた所、フランスでは(カフェなどのフランクな場は除く)外食を1人でする文化はないと出てくるし、単に欧米文化の特徴なのかもしれない。だとすれば日本人が考えている以上に、学会なんかのレセプションに出席して親交を深めることは重要な事項なのだろう*16。同室の学生の言うところによると「食事は社会活動*17なんだから一緒に食べないとダメでしょ」ということだ。

一人暮らしと猫

日本ではずっと実家ぐらしだったので、一人暮らしに悪戦苦闘している。

ヨーロッパのキャベツは固い。調理に困った。
出汁をなくして、初めて重要さに気がついた。
表示がオランダ語/フランス語なので、野菜はともかく、肉は全く分からない。

だがしかし、下宿先に猫が居り、今まで叶わなかった猫との生活が達成できた。僥倖である。

f:id:ajhjhaf:20180116011938j:plain

物凄く嫌がられている気がしなくもない。

結び

こちらの滞在も半分を切った。なんとかハイパフォーマンスの方法論の欠片でも掴みたい。

履歴

2018-01-17: どうやって行ったか、の題と文が合ってなかったので追記 2018-01-30: 読み返して恥ずかしくなった部分を削除

*1:自宅から空港+往復航空券+空港から下宿先

*2:家賃+研究室までの定期券

*3:自分もそんなイメージだった

*4:特に当時のエリートはフランス語を用いたため、高級階層はフランス語がメインだったんだとか。

*5:MITはR&Dに931億円を使ったらしい。。

*6:個人的な物言いだが、博士課程への警告は山ほど目にし耳に入ってくるものの、卒業要件について確認するべきとの声を聞いたことはない。この基準は大学毎、時により研究科毎にかなり異なる。機関によっては査読付き論文が必要がないところもあるし、逆に3報の筆頭著者論文(化学系など)が必要な場合もある。もし読者が博士課程に進学する際には、ゆめゆめ確認して欲しい。

*7:このような状況にあり、学位が取得できていない学生は研究科に複数実在する。

*8:逆に指導教員の決定次第で学位取得がかなり容易にもなりうる。しかし分散が大きいだけなので品質保証としてはやはり良くない

*9:なんでも指導教員も自身がこちらで取り組んでいる研究には関わっているらしく著者に入るらしい

*10:勿論研究者として生きていくことを考えるなら、別である。良い論文を出せる確率がある。

*11:中途半端ともいう

*12:bioinformaticsだと研究成果について生物学的な知見が要る。そのため大体1~2年かかるイメージだ。一方でcomputational biologyだと計算機科学の観点が強く、上手く行けばこの短期でも論文になろう。

*13:なので自分の専門はbiostatistics、あるいはtablomicsかdatabasomicsなどと述べていた

*14:同室の学生は「金曜日には16:30でも帰るには遅すぎる」という名言を残した

*15:University Research Administrator。日本でのURAの働きは、遺伝研の要覧が分かりやすい。獲得したグラントや出版論文が丁寧に纏めてあり機関の重要性がよく伝わる。

*16:現状の日本の制度では、懇親会費は個人の自腹となっている

*17:social activity

2017-08-05

Stanで生存時間解析(Weibull 回帰)

ベイジアンモデリング

生存時間解析とは？

生存時間解析は、イベントの時間を解析するための手法です。例えば、

ソーシャルゲームやwebサービスなどに登録した人の利用継続時間(マーケティング)
投薬群と対照群(プラセボ)で、どれだけ長生きするか(医用統計)
新規材料が既存の材料とくらべて、どれぐらい耐久性があるか(信用工学)

など、様々な応用例が考えられます。生存時間解析はノンパラメトリックな手法で行なうことが多いです。具体的には、

カプランマイヤー推定量で生存時間を推定
生存時間の違いをログランク検定で判断
共変量の違いをCoxの比例ハザードモデルやAelanの加法モデルで解析

といった辺りが挙げられるでしょうか。その原因としては、生存時間のデータへ打ち切りという特徴があることが挙げられます。結果として分布にあてはめるだけの解析では、打ち切りを説明することが難しく上手くフィッティング出来ません。並べて、最尤法を使った分布への当てはめでは、値の信頼性が出ません。これに対してノンパラメトリックなカプランマイヤー法を使えば、推定値の範囲(信頼性)も出せますので論文も書きやすいです。

しかし仮に分布を仮定しても、ベイズ的にモデリングすれば、これらの問題を解決することができます。今回はStanを使って生存時間解析を行なうことで、打ち切りを含めてモデリングをしてみました。何分不勉強なもので、ご指導ご鞭撻をいただければ幸いです。

テストデータ

とりあえず解析に使うデータを用意します。今回はpythonのlifeline packageに含まれる、rossiのデータを使います。データのソース論文はこちらです。このデータは逮捕された人が再逮捕されるまでの期間(週)と、その他の共変量が記されています。何はともあれ、データを見てみましょう。上から10件だけ表示します。

from lifelines.datasets import load_rossi

df = load_rossi()
df

index	week	arrest	fin	age	race	wexp	mar	paro	prio
0	20	1	0	27	1	0	0	1	3
1	17	1	0	18	1	0	0	1	8
2	25	1	0	19	0	1	0	1	13
3	52	0	1	23	1	1	1	1	1
4	52	0	0	19	0	1	0	1	3
5	52	0	0	24	1	1	0	0	2
6	23	1	0	25	1	1	1	1	0
7	52	0	1	21	1	1	0	1	4
8	52	0	0	22	1	0	0	0	6
9	52	0	0	20	1	1	0	0	0
10	52	0	1	26	1	0	0	1	3

詳細は論文の3.2節に書いてありますが、今回注目するのはweekとarrestです。arrestが1である人は再逮捕されています。0である人は観測期間中では再逮捕はされず、weekの値が52になっています。所謂打ち切りの発生です。

モデル

アヒル本P115 7.8 打ち切り、に従い、現象をモデル化してみます。なお今回のデータはweek単位への丸めも発生しているのですが、本題ではないので飛ばします。

StanとRでベイズ統計モデリング (Wonderful R)

作者:松浦健太郎
出版社/メーカー: 共立出版
発売日: 2016/10/25
メディア: 単行本

打ち切りの原理を踏まえて、今回の現象のモデルを次のように考えました。

「再逮捕の区間を表すパラメータと分布に従って、再逮捕までの時間 $y$ が得られる。ただし $52 \lt y$ である場合は、 $y = 52$ とする」

分布はワイブル分布を利用します。ワイブル分布は次のような特徴をもち、時間のモデル化へ向いています。

$0 \lt t \lt \infty$ における累積密度関数の和が1になる(イベントの発生確率を無限時間まで考えられる)
現象の傾向を示す形状パラメータと、現象の時間スケールを示す尺度パラメータで表現される
- $m \lt 1$ なら、時間とともにハザード関数値(時間 $t$ までにイベントが発生しなかった場合、その瞬間にイベントが起こる確率)が低くなる
- $m = 1$ なら、時間に依らずハザード関数値が一定
- $m \gt 1$ なら、時間にとともにハザード関数値が高くなる

ワイブル分布を使って、値に対する尤度を考えます。観測値が52で無い場合は

$weibull\_lpdf(y|m, \eta)$

として得られます。肝心なのは52の場合です。この時尤度は

$\begin{align} Prob[52 \lt y] &= \int_{52}^{\infty}weibull(52|m, \eta) \\\ &= 1 - \int_0^{52} weibull(52|m, \eta) \\\ &= 1 - weibull\_cdf(52|m, \eta) \\\ &= weibull\_ccdf(52|m, \eta)\end{align}$

となります。

以上を踏まえて、まず共変量に依らず、全ての人が共通の現象に従っているとして、Stanを書いてみました。

data {
    int N ;
    int week[N] ;
    int arrest[N] ;
}

parameters {
    real shape ;
    real scale ;
}

model {
    for(n in 1:N){
        if(arrest[n] == 0){
            target += weibull_lccdf(week[n]| shape, scale) ;
        }else{
            target += weibull_lpdf(week[n]| shape, scale) ;
        }
    }
}

generated quantities {
    real log_lik[N] ;
    for(n in 1:N){
        if(arrest[n] == 0){
            log_lik[n] = weibull_lccdf(week[n]| shape, scale) ;
        }else{
            log_lik[n] = weibull_lpdf(week[n]| shape, scale) ;
        }
    }
}

解析と可視化

データに対して、構築したStanモデルを当てはめてみます。

import numpy as np
import os 
import pystan
import pandas as pd
import pickle
from lifelines.datasets import load_rossi


def stan_compile(stan_file_path, compiled_file_path, recompile=False):
    if os.path.exists(compiled_file_path) is False or recompile is True:
        model = pystan.StanModel(file=stan_file_path)
        with open(compiled_file_path, "wb") as f:
            pickle.dump(model, f)
    else:
        with open(compiled_file_path, "rb") as f:
            model = pickle.load(f)
    return model 

def get_summary_df(fit):
    summary = fit.summary(probs=prob)
    summary_df = pd.DataFrame(summary["summary"],
                              index=summary["summary_rownames"],
                              columns=summary["summary_colnames"])
    return summary_df

def get_waic(fit):
    log_lik = fit.extract("log_lik")["log_lik"]
    waic = (-2 * np.sum(np.log(np.mean(np.exp(log_lik), axis=0))) +
            2 * np.sum(np.var(log_lik, axis=0))) 
    return waic

# Stanに入れるデータの準備
df = load_rossi()
N = len(df)
week = df["week"]
arrest = df["arrest"]
stan_data = {"N": N, "week": week, "arrest": arrest}
prob = [0.025, 0.05, 0.25, 0.5, 0.75, 0.95, 0.975]

# Stanをコンパイル
stan_file = os.path.join("weibull.stan")
stan_file_c = os.path.join("weibull.pkl")
model = stan_compile(stan_file, stan_file_c)

# StanへKick
fit = model.sampling(data=stan_data,
                     iter=3000,
                     chains=5,
                     warmup=1000,
                     seed=1234)

# 結果の集計
summary_df = get_summary_df(fit)
waic = get_waic(fit)
print(waic)
summary_df

output

WAIC: 1397.22843377

parameter	mean	se_mean	sd	2.5%	5%	25%	50%	75%	95%	97.5%	n_eff	Rhat
shape	1.35177	0.00225134	0.123002	1.12027	1.15716	1.26817	1.347	1.43093	1.56233	1.61164	2985	1.00366
scale	127.559	0.267877	14.5396	103.759	106.833	117.305	125.893	136	153.639	161.079	2946	1.00274
log_lik[0]	-5.26822	0.000938137	0.0870498	-5.44863	-5.41606	-5.3248	-5.26577	-5.20816	-5.13211	-5.10419	8610	0.999675
log_lik[1]	-5.30895	0.000968553	0.0933687	-5.5044	-5.46746	-5.36939	-5.30494	-5.2457	-5.16148	-5.13464	9293	0.999847
log_lik[2]	-5.21905	0.00110178	0.0852228	-5.39228	-5.36399	-5.27516	-5.21646	-5.16062	-5.08346	-5.05936	5983	1.00011
…	…	…	…	…	…	…	…	…	…	…	…	…

まず集計表です。全パラメータで $\hat{R} \lt 1.1$ が確認できましたので、収束は問題ないようです。続いて、得られたパラメータ値を用いて可視化を行います。

from scipy.stats import weibull_min
import matplotlib.pyplot as plt


# 可視化その1
fig, ax1 = plt.subplots()
x = np.arange(0, 500, 1)
y = weibull_min.pdf(x, c=summary_df.loc["shape", "mean"], scale=summary_df.loc["scale", "mean"])
y_min = weibull_min.pdf(x, c=summary_df.loc["shape", "mean"], scale=summary_df.loc["scale", "5%"]) 
y_max = weibull_min.pdf(x, c=summary_df.loc["shape", "mean"], scale=summary_df.loc["scale", "95%"]) 
# 確率密度関数
ax1.plot(x, y, "-")
ax1.fill_between(x, y_min, y_max, facecolor="pink")
ax1.set_ylabel("probability")
ax1.tick_params("y")
ax1.set_xlabel("Weeks")
# 件数
ax2 = ax1.twinx()
ax2.hist(df["week"])
ax2.set_ylabel("count")
ax2.tick_params("y")
plt.show()

# 可視化その2
fig, ax1 = plt.subplots()
x = np.arange(0, 50, 1)
y = weibull_min.sf(x, c=summary_df.loc["shape", "mean"], scale=summary_df.loc["scale", "mean"])
y_min = weibull_min.sf(x, c=summary_df.loc["shape", "mean"], scale=summary_df.loc["scale", "5%"]) 
y_max = weibull_min.sf(x, c=summary_df.loc["shape", "mean"], scale=summary_df.loc["scale", "95%"]) 
# 生存時間関数
ax1.plot(x, y, "-")
ax1.set_ylabel("Propotion Not Arrested")
ax1.fill_between(x, y_min, y_max, facecolor="pink")
ax1.set_xlabel("Weeks")
ax1.tick_params("y")

f:id:ajhjhaf:20170805173622p:plain

f:id:ajhjhaf:20170805173634p:plain

一枚目のグラフが、確率密度関数とイベント発生のカウントです。MCMCのEAPが青線、scale parameterの90%信用区間を用いて描かれた範囲がピンク色になっています。

二枚目のグラフが生存時間関数(survival function)です。見方は1枚目と同様です。元論文のP7には、Coxの比例ハザードモデルで描かれた場合の結果が載っています。今回のWeibull分布を用いて描いた結果と相違ありません。

打ち切り補正をしない場合は？

当然ここで気になってくるのは、補正の効果です。先程の1枚目のグラフは52辺りに最頻値があります。打ち切りをしている効果はどの程度でしょうか？これを検証するために、打ち切りを考慮しないモデルと比較しました。

f:id:ajhjhaf:20170805175603p:plain

打ち切りを考慮しない場合は、めちゃめちゃ過剰適合しているのがわかります。打ち切りのメカニズムをモデルに取り入れることで、52以上でもイベントが生起することを踏まえてモデル化できてるわけですね。ちなみに打ち切りが考慮されない場合、WAICも3411.15613467となり、モデルとしても性能が良くないことが分かります。

比例ハザードモデル

次に共変量の効果を調べます。一番単純な比例ハザードモデルで取り組んでみましょう。比例ハザードモデルは、全時間を通してハザード間数値を一定として、共変量に従ってハザード関数の値が大きくなることを仮定するモデルです。Weibull分布のハザード関数は

$\begin{align} h(t|m, \eta) &= \frac{m}{\eta}(\frac{t}{\eta})^{m-1} \\\ &= \frac{m}{\eta^m}t^{m-1} \\\ &= m \lambda t^{m-1} \\\ \end{align}$

と示されます。先行研究[1][2]では、尺度パラメータ $\eta$ へ共変量の効果を加えています。この理由の僕個人による定性的な理解としては、形状パラメータの頑強性に帰するものと考えています。形状パラメータの値はそもそもの現象に依存します。共変量ぐらいでは、中々現象の傾向までは大きく変わりません。

更に、尺度に対する効果も尺度パラメータ $\eta$ へダイレクトに加えるのではなく、 $\lambda$ へ加えるほうが多いようです。即ち基底状態に対するパラメータを $\beta_0$ 、共変量の係数を $\beta$ 、共変量のダミー変数を $F$ として、

$\lambda = exp(\beta_0 + \beta^TF )$

ということになります。この式を $\eta$ を中心に変形すれば

$\eta = exp(-\frac{\beta_0 + \beta^TF}{m})$

です。Stanで実装するときは、この式で書けばよいかと思います。

今回の解析では、逮捕後の経済的支援(financial aid)の効果を調べてみたいと思います。モデルは次の通りです。

data {
    int N ;
    int week[N] ;
    int arrest[N] ;
    int fin[N] ;
}

parameters {
    real shape ;
    real beta[2] ;
}

model {
    for(n in 1:N){
        if(arrest[n] == 0){
            target += weibull_lccdf(week[n]| shape, exp(- (beta[1] + fin[n] * beta[2]) / shape)) ;
        }else{
            target += weibull_lpdf(week[n]| shape, exp(- (beta[1] + fin[n] * beta[2]) / shape)) ;
        }
    }
}

generated quantities {
    real log_lik[N] ;
    for(n in 1:N){
        if(arrest[n] == 0){
            log_lik[n] = weibull_lccdf(week[n]| shape, exp(- (beta[1] + fin[n] * beta[2]) / shape)) ;
        }else{
            log_lik[n] = weibull_lpdf(week[n]| shape, exp(- (beta[1] + fin[n] * beta[2]) / shape)) ;
        }
    }
}

スクリプトは殆ど同様なので飛ばします。結果として次のグラフが得られました。

f:id:ajhjhaf:20170805185919p:plain

f:id:ajhjhaf:20170805185927p:plain

2枚目のグラフが分かりやすいですね。経済的支援を受けた場合は、再犯率が低くなっています。WAICも1395.3474841となって低くなり、予測力が上がっています。更に言うと、経済的支援の効果を表すパラメータ $\beta_1$ に対する、 $exp(\beta_1)$ の95%信用区間(片側)は $0.502 \lt exp(\beta_1) \lt 0.948$ でした。この区間に1(即ち効果が無い)が入っていませんので、経済的支援に効果があったことが期待されます。

まとめ

Python + Stan + Weibull分布を使って、打ち切りを含めたモデル化を行い、共変量の効果の信用区間まで計算しました。…あれ、これはCoxの比例ハザードモデルで十分なのでは(死)。

ベイズ的にモデル化することの利点は自由性です。パッと思いつくものとして、次のような応用が挙げられます。

加法モデルやオッズ比モデルの利用
値の丸めを加味したモデル
時間tに対して、ハザード関数が変化するモデル(比例ハザードモデルでは一定とする)
リンク関数の中身へ正規化項を追加して、スパースにする(Lasso + weibull 回帰？)
単純な2群比較のコホートデザインではない場合(利用できる共変量が他にある)

ふぅー、これでやった意味が見いだせました。ぜひ皆様も、Weibull分布に親しんで下さい。

参考

書籍

実践ベイズモデリング -解析技法と認知モデル-

作者:豊田秀樹
出版社/メーカー: 朝倉書店
発売日: 2017/01/25
メディア: 単行本（ソフトカバー）

2節「ワイブル分布」がドンピシャでした。

StanとRでベイズ統計モデリング (Wonderful R)

作者:松浦健太郎
出版社/メーカー: 共立出版
発売日: 2016/10/25
メディア: 単行本

打ち切りデータのモデリングについて勉強させて貰いました。

Webリソース

2017-06-25

StanとPythonでベイズ統計モデリング　その3　Chapter6

ベイジアンモデリング

アヒル本(StanとRでベイズ統計モデリング)のChapter6にPythonで取り組んでいきます。この章は丁寧に分布を解説していくものなので、内容の復習は飛ばします。おざなりにされそうな章ですが、自分でパラメータをいじって分布からサンプリングしてみると新しい発見もありますので挑戦してみるのをおすすめします。

今回はRどころかStanも出てきません(笑)

練習問題

練習問題(1)

ベルヌーイ分布 or カテゴリカル分布に従う乱数を生成せよ…ということですが、numpyには両方とも存在しません。二項分布からのサンプリングを一回だけ行うものがベルヌーイ分布であり、多項分布からのサンプリングを一回だけ行うものがカテゴリカル分布であるため、それで代用しました。

カテゴリカル分布についてはRの結果と対応させるために少し手間を加えます。

import numpy as np

random_bernoulli = np.random.binomial(1, 0.5, 100)

random_categorical = np.random.multinomial(1, [0.2, 0.3, 0.5], 100)
np.where(random_categorical == 1)[1]

練習問題(2)

テキストで推奨されている、ベータ分布、ディリクレ分布、ガンマ分布、2変量正規分布、コーシー分布を生成していきます。ついでに可視化します。

ベータ分布

alphaが大きいほど右側に偏り、全体的に値が大きいほど真ん中(0.5辺り)に集合していくことが分かりました。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

alpha = 0.5
beta = 0.5
r_beta = np.random.beta(alpha, beta, size=1000)
g = sns.distplot(r_beta, kde=False, label="alpha={0}, beta={1}".format(alpha, beta))

alpha = 1 
beta = 0.5
r_beta = np.random.beta(alpha, beta, size=1000)
g = sns.distplot(r_beta, kde=False, label="alpha={0}, beta={1}".format(alpha, beta))

alpha = 1 
beta = 1 
r_beta = np.random.beta(alpha, beta, size=1000)
g = sns.distplot(r_beta, kde=False, label="alpha={0}, beta={1}".format(alpha, beta))

alpha = 5 
beta = 5 
r_beta = np.random.beta(alpha, beta, size=1000)
g = sns.distplot(r_beta, kde=False, label="alpha={0}, beta={1}".format(alpha, beta))

g.legend()
plt.show(g)

f:id:ajhjhaf:20170531172702p:plain

ディリクレ分布

トピックモデルで使われる分布です。ベータ分布の多次元拡張なので、alphaに対する挙動はベータ分布と同じです。

今回は3次元で行いました(可視化の限界のためです…)。可視化の方法は先行事例を参考にしています。

import matplotlib.tri as tri
import numpy as np

def plot_points(X, barycentric=True, border=True, **kwargs):
    '''
    Copy from https://gist.github.com/tboggs/8778945
    '''
    corners = np.array([[0, 0], [1, 0], [0.5, 0.75**0.5]])
    triangle = tri.Triangulation(corners[:, 0], corners[:, 1])
    if barycentric is True:
        X = X.dot(corners)
    plt.plot(X[:, 0], X[:, 1], 'k.', **kwargs)
    plt.axis('equal')
    plt.axis('off')
    plt.xlim(0, 1)
    plt.ylim(0, 0.75**0.5)
    if border is True:
        plt.triplot(triangle, linewidth=1)
        
fig = plt.figure()
ax = fig.add_subplot(2,2,1)
alpha=[3,3,3]
r_diri = np.random.dirichlet(alpha, size=1000)
ax.set_title("alpha={0}".format(alpha))
plot_points(r_diri)

ax = fig.add_subplot(2,2,2)
alpha=[0.3,0.3,0.3]
r_diri = np.random.dirichlet([0.3,0.3,0.3], size=1000)
ax.set_title("alpha={0}".format(alpha))
plot_points(r_diri)

ax = fig.add_subplot(2,2,3)
alpha=[3,0.3,0.3]
r_diri = np.random.dirichlet([3,0.3,0.3], size=1000)
ax.set_title("alpha={0}".format(alpha))
plot_points(r_diri)

ax = fig.add_subplot(2,2,4)
alpha = [1,1,1]
r_diri = np.random.dirichlet([1,1,1], size=1000)
ax.set_title("alpha={0}".format(alpha))
plot_points(r_diri)
plt.show()

f:id:ajhjhaf:20170531172713p:plain

ガンマ分布

ガンマ分布は離散値を取る分布です。numpyの場合はshapeとscaleの２つのパラメータをとるのですが、scaleは教科書の $\beta$ の逆数になります。というわけで

平均値は $shape * scale$
標準偏差は $\sqrt{shape}*scale$

になります。ご注意下さい。

shape = 5
scale = 5
r_gamma = np.random.gamma(shape, scale, size=1000)
g = sns.distplot(r_gamma, label="shape={0}, scale={1}".format(shape, scale), kde=False)

shape = 5
scale = 20 
r_gamma = np.random.gamma(shape, scale, size=1000)
g = sns.distplot(r_gamma, label="shape={0}, scale={1}".format(shape, scale), kde=False)

shape = 40 
scale = 5
r_gamma = np.random.gamma(shape, scale, size=1000)
g = sns.distplot(r_gamma, label="shape={0}, scale={1}".format(shape, scale), kde=False)

g.legend()
plt.show()

f:id:ajhjhaf:20170531174245p:plain

2変量正規分布

平均と分散にどう2変量が関わるか示す相関係数を入れ込みます。共分散行列の書き方はもっと綺麗なものがありそうですが。。

import seaborn as sns
import matplotlib.pyploy as plt
import numpy as np

mu1 = 5
mu2 = 5
sigma1 = 10
sigma2 = 40
rho = 0.6
mu = np.array([mu1, mu2])
cov = np.array([[sigma1**2, sigma1*sigma2*rho], [sigma1*sigma2*rho, sigma2**2]])
r_mnorm = np.random.multivariate_normal(mu, cov, size=1000)

g = sns.jointplot(r_mnorm[:, 0], r_mnorm[:, 1], kind="kde", n_levels=50)
plt.show(g)

f:id:ajhjhaf:20170531172724p:plain

コーシー分布

numpyではパラメータを選べない標準コーシー分布しか使えません。そのためscipyを利用しました。

なおここまでのnumpyで生成した他の分布も、rvs(random variates sampling?)メソッドを使えば同様に得ることが出来ます。ただnumpyとscipyで仕様が異なり、numpyの正規分布を由来とする乱数はnumpy.random.normalなのに、scipyはscipy.stats.normだったりします(解せぬ)。

コーシー分布は面白い分布ですね。パラメータがあるものの、平均値や分散をそこから推定できない。しかもめちゃめちゃ変なところに外れ値みたいに値が登場する性質を持っています。

import seaborn as sns
import matplotlib.pyploy as plt
from scipy.stats import cauchy

r_cauchy = cauchy.rvs(0, 1, 100)
sns.distplot(r_cauchy)
plt.show()

f:id:ajhjhaf:20170531172819p:plain

練習問題(3)

$x_1 - x_2 \sim Normal(\mu_1 - \mu_2, \sqrt{\sigma_1^2 + \sigma_2^2 - 2\rho\sigma_1\sigma_2})$ のような分布になります。これは以前に触れた部分ですね。

正規分布の線形結合で表される分布は、記事内のpdfを読めば全部同じように表されることが分かります。

y1 = np.random.normal(50, 20, 2000)
y2 = np.random.normal(20, 15, 2000)
diff = y1 - y2
sns.distplot(diff)
plt.show()

f:id:ajhjhaf:20170531172937p:plain

練習問題(4)

何か自分でテキストに載っていない分布を対象にすること。という問題でした。

今回は負の二項分布を取り扱ってみます。生物学の分野では、遺伝子発現量(RNA-seq or cDNA-seq)の推定モデル(DESeqやedgeR)でよく使われている分布です。負の二項分布はポアソン分布とガンマ分布の混合モデルです。ホクソエムさんの分かりやすい解説があるので、そちらをご覧ください。ポアソン分布の $\gamma$ が確率的に変動することで、過分散に対応できるようになっています。

負の二項分布の解説は英語版Wikipediaを見るのが一番いいと思います。以下そこからのざっくりとした抽出です。

「負の」の意味

負の二項分布は定義4パターン存在します。4つはそれぞれ

成功率pの試行をr回失敗(成功)するまでに、成功(失敗)した回数kの分布
成功率pの試行をr回失敗した時の、試行回数nの分布
成功率pの試行をk回成功した時の、失敗回数rの分布
成功率pの試行をk回成功した時の、試行回数nの分布

となります。4つのパターンがありますが、一番良く使われるのは1つ目のものです。

1つ目のパターンを式で表すと、

f:id:ajhjhaf:20170603170330p:plain:w300

となります。このパターンは試行が成功でも失敗でも式に大きな変化がなく、逆で紹介されている場合もあります。その時は逆側の事象が起こる確率が1-pになるように対応が変化するだけです。ところで、成功回数と失敗回数の和が試行回数です。つまり $n = k + r$ となります。これを使って整理すると

f:id:ajhjhaf:20170603171743p:plain:w300

となりました。ところで普通の二項分布の式は次のようになります。

f:id:ajhjhaf:20170603171236p:plain:w300

つまり負の二項分布だと二項分布と比べてトライアル $n$ の数が-1されていることになります。

平均と分散

負の二項分布の平均と分散は次のようになります。

$\mu = \frac{pr}{1-p}$

$var = \mu(1+\frac{\mu}{r})$

詳しい導出についてはこちらを参考にするのが適切だと思いました。日本語版Wikipediaの記事は、どこか間違っているような…。

実数への拡張

負の二項分布のパラメータ $r$ は正の実数へ拡張することが出来ます。「rが実数の『成功率pの試行をr回失敗(成功)するまでに、成功(失敗)した回数kの分布』ってなんやねん」と僕は思いました。おそらくここで肝心なのは、 $r$ を正の実数に拡張しても元々の定義へ矛盾せずに一般化できるということではないかと思います。この時ガンマ関数 $\Gamma()$ を利用して、

$NegativeBinomial(k|n, p) \sim \frac{\Gamma(n)}{k!\Gamma(n-k)}$

のように書くことが出来ます。

平均と形状パラメータによる分布の指定

負の二項分布のパラメータを指定する時に $n, p$ ではなく、平均パラメータ $\mu$ と形状パラメータ $\alpha$ を使って記述されることがあります。形状パラメータとは分散をスッキリさせるために $r$ の逆数を取って $\alpha = \frac{1}{r}$ としたものです。一応形状パラメータと書きましたが、他にも呼び方が色々あり、

shape parameter
dispersion parameter
clustering coefficient
heterogeneity
aggregation

のようにとりとめがありません。文字の使い方も適当らしく、論文によっては $\phi$ が使われているものもありました。

分布の可視化

可視化をする時にbinsを自分で指定しています。何も指定しないと最適なbinsをseabornが決めてくれるのですが、範囲が小数で分割された場合には離散値である負の二項分布の値がダブルカウントされるのか、物凄く変な分布になってしまいます。気をつけて下さい。

import numpy as np
from scipy.stats import nbinom
import seaborn as sns
import matplotlib.pyplot as plt

# r_nb = np.random.negative_binomial(10, 0.3, 10000)
r_nb = nbinom.rvs(10, 0.3, size=10000)

sns.distplot(r_nb, kde=False, bins=np.arange(0,100,5))
plt.show()

f:id:ajhjhaf:20170531193122p:plain

余談ですがedgeRの論文は事実上、RNA-seqの解析に負の二項分布をあてはめだだけの論文です。2ページしかありません。そのわりに1000回を超えれば場外ホームランとなる世界で、2500回も引用されている(Scopus調べ)ので、なんとも夢があります。

2017-06-16

StanとPythonでベイズ統計モデリング　その2　Chapter5

ベイジアンモデリング

アヒル本(StanとRでベイズ統計モデリング)のChapter5にPythonで取り組んでいきます。練習問題を解いて、本文中に書かれてるグラフをPythonで描いてみます。

なおChapter1~3は導入だったのと、Chapter4は練習問題の内容が「はじめての統計データ分析」と被っていたのでパスします。

Chapter5 基礎的な回帰とモデルのチェック

重回帰
- 複数の説明変数を用いた回帰のこと
  - 重回帰も結局は正規分布を仮定している
- 目的
  - 説明変数からの応答変数の予想、及び説明変数の寄与率
- 分布
  - 複数の説明変数ならScatterplot matrixを利用すると良い
- MCMCの設定について
  - スケーリング: MCMCを行う前に、各データのオーダーを大体(1前後に)そろえること。
    - 収束がしやすく、早くなる
    - 最大値、標準偏差、標準偏差の倍で割ったりすれば良い
- 結果の解釈 : モデルの改善に活かす!
  - 因果関係の推定
    - どちらが先に起こりうるか、といった事前知識が必要
  - 外挿
    - 利用したデータが $a \lt x \lt b$ の範囲であるにも関わらず、 $c \lt\lt a$ のようなデータ $c$ をモデルに当てはめて予測することを外挿と呼ぶ。大体は予想外のデータなので、上手く行かない。
  - パラメータの幅
    - EAPなどの点推定量より、幅がどうなっているかが大事(0を跨いだりしていないか？)
  - 可視化
    - 実測値と予測値のプロット(データと予測分布)
      - X軸にデータ、Y軸にEAPから得られる予測値をプロット
      - y = xの直線から大きく外れることがなければOKとする
    - 推定ノイズの分布
      - ノイズの分布を仮定した時に、それがモデルに従っているか確認する
  - MCMCサンプルの散布図行列
    - パラメータの関係について読み取れる
(二項)ロジスティック回帰
- ロジスティック関数をつかった方法
  - 応答変数が0から1の間にある場合、説明変数に適用することで値の範囲を変換することが出来る
- 2項分布モデル
  - 正規分布が当てはまらない場合には特に有効
  - 値が整数で幅が小さく、連続値とみなせないような場合に使う
  - Nが十分に大きい場合は正規分布に近似できる(正規分布の方が演算が高速なのでよい)
- ベルヌーイ分布モデル
  - 応答変数がbool値であるような時にはベルヌーイ分布を利用すれば良い
- 生成量
  - オッズ
    - 二項ロジスティック回帰モデルにおいて、 $Y \sim Binomial(M, q)$ であり、 $q = \frac{1}{1+\exp(-x)}$ であるならば $\frac{q}{1-q} = exp(x)$ と変換することが出来る
    - $\frac{q}{1-q}$ はオッズと呼ばれる
    - その事象が起こるサンプリング確率の比率を示す
- 可視化
  - ベルヌーイ分布を利用した場合
    - $Y \sim Bernoulli(q)$ より推定されたqを利用する
    - 判断基準の閾値cを決定して、qとcからTP, FP, FN, TNの計算を行う
    - FP, TPを各qについてplotして曲線(ROC)を書く
    - ROCを下回った部分がAUCで、0.8以上だと良いものとされる
ポアソン回帰
- カウントデータに対して予測を行う時に用いる
  - $Y \sim poisson(\lambda)$ でカウントデータYが決定されるものとして、 $\lambda$ は説明変数の線形結合を0以上に変換したものを使う( $exp(x)$ がよく使われる)
  - パフォーマンスの理由より、 $\lambda$ が十分に大きいなら、正規分布で近似して良い

練習問題

Scatterplot matrixについて

Pythonの実装はpandasマスターのid:sinhrksさんの記事を見るのが良いと思います。

sinhrks.hatenablog.com

個人的な使った感想は次の通りです。

離散値の可視化が上手く行かないことがある(6離散値指定したのに、4つしか表示されないことがある)？
- たぶんこれはseabornのPairPlotのバグです……
- 離散値/連続値判定の初期値が大きすぎると上手くいかないので、離散値の判定閾値を4, 5辺りにいじって使いました。
離散値の場合は対角のカウントはcountplotを使ったほうが良い？
- 他の下半分、上半分のグラフと軸を合わせやすくするためです。
- どうせseabornはPairGridで使うことになりますし…

そういうわけで改造させて頂いたバージョンがこちらです。残念ながら1つ目のバグは取れていません。そもそも僕の環境に特有なのかもしれませんし、諦めました。上三角行列の部分はid:statmodelingさんの記事のまんまです。

statmodeling.hatenablog.com

#!/usr/bin/env python
# vim:fileencoding=utf-8
# Created: 2017-06-06
# Original scripts: http://sinhrks.hatenablog.com/entry/2016/11/01/075527

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib.patches import Ellipse


class Dispatcher(object):

    def __init__(self, fontsize=20, alpha=0.6, cmap='RdBu', threshold=5):
        self.fontsize = fontsize
        self.alpha = alpha
        self.cmap = plt.get_cmap(cmap)

        # 離散値 / 連続値とみなす閾値
        self.threshold = threshold

    def comb(self, x_series, y_series, label=None, color=None):
        """ 下三角部分のプロット """

        x_nunique = x_series.nunique()
        y_nunique = y_series.nunique()

        if x_nunique < self.threshold and y_nunique < self.threshold:
            # 離散値 x 離散値のプロット
            return self._dd_plot(x_series, y_series, label=label, color=color)

        elif x_nunique < self.threshold or y_nunique < self.threshold:
            # 離散値 x 連続値のプロット
            return self._dc_plot(x_series, y_series, label=label, color=color)

        else:
            # 連続値 x 連続値のプロット
            return plt.scatter(x_series, y_series, label=label, color=color)

    def _dd_plot(self, x_series, y_series, label=None, color=None):
        """ 離散値 x 離散値のプロット """

        # x, y 各組み合わせの個数を集計
        total = y_series.groupby([x_series, y_series]).count()

        # x, y軸をプロットする位置を取得
        xloc = total.index.labels[0]
        yloc = total.index.labels[1]
        values = total.values

        ax = plt.gca()
        for xp, yp, vp in zip(xloc, yloc, values):
            ax.annotate(vp,
                        (xp, yp),
                        fontsize=self.fontsize,
                        ha='center',
                        va='center')

        # 組み合わせの個数を散布図としてプロット
        size = values / (values.max() * 1.1) * 100 * 20
        ax.scatter(xloc, yloc, s=size, label=label, color=color)
        ax.set_ylim(yloc[0] - 0.5, yloc[-1] + 0.5)

    def _dc_plot(self, x_series, y_series, label=None, color=None):
        """ 離散値 x 連続値のプロット """

        if y_series.nunique() < x_series.nunique():
            # y軸が離散値の場合は、x, yを入替
            # 水平方向に箱ひげ図をプロット
            orient = "h" 
        else:
            orient = "v" 

        ax = sns.boxplot(x_series, y_series, orient=orient, color=color)
        ax = sns.swarmplot(x_series, y_series, orient=orient, color=color) 

    def diag(self, x_series, label=None, color=None):
        """ 対角部分のプロット """

        x_nunique = x_series.nunique()
        if x_nunique < self.threshold:
            ax = sns.countplot(x_series, color=color)
        else:
            ax = sns.distplot(x_series, kde=False, color=color)
        ax.yaxis.set_visible(False)

    def ellipse(self, x_series, y_series, label=None, color=None):
        """ 上三角部分のプロット """

        # 相関係数を楕円としてプロット
        r = x_series.corr(y_series)
        c = self.cmap(0.5 * (r + 1))
        ax = plt.gca()
        ax.axis('off')
        artist = Ellipse(xy=[.5, .5],
                         width=np.sqrt(1+r),
                         height=np.sqrt(1-r),
                         angle=45,
                         facecolor=c,
                         edgecolor='none',
                         transform=ax.transAxes)
        ax.add_artist(artist)
        ax.text(.5,
                .5,
                '{:.0f}'.format(r*100),
                fontsize=28,
                horizontalalignment='center',
                verticalalignment='center',
                transform=ax.transAxes)

       
d = Dispatcher()

# データを作る
x = np.random.normal(100, 5, 30)
y = np.random.choice([1,2,3], 30, p=[0.1,0.2,0.7])
z = np.random.choice([1,2,3,4], 30, p=[0.2,0.2,0.2,0.4])
w = np.random.normal(4, 0.1, 30)
df = pd.DataFrame(np.array([x,y,z,w]).T, columns=["x", "y", "z", "w"])

# 可視化する
g = sns.PairGrid(df, diag_sharey=False)
g.map_diag(d.diag)
g.map_lower(d.comb)
g.map_upper(d.ellipse)
plt.show()

f:id:ajhjhaf:20170606191215p:plain

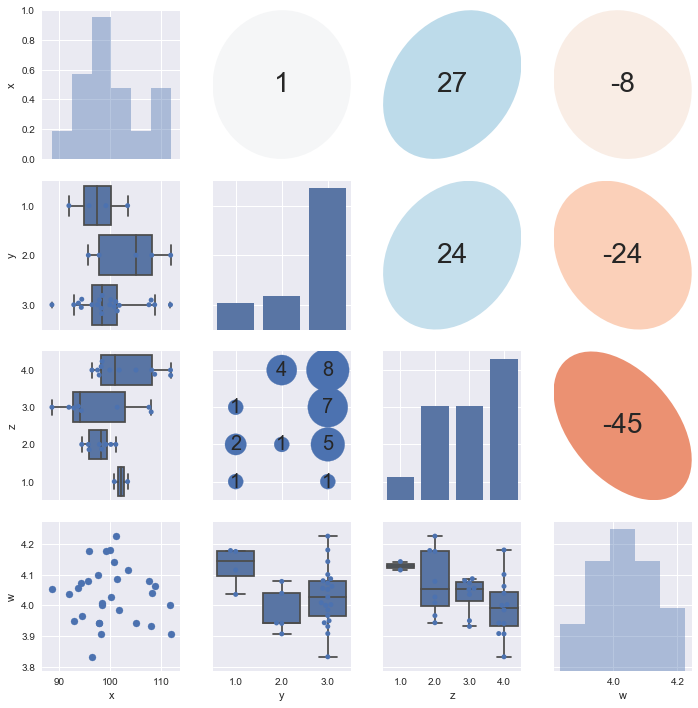
これとは別に、勉強として自分でも実装してみましたが、離散×離散の可視化が難しいところです。僕はヒートマップを使おうかと思ったのですが、軸を表示しようとする関係でズレます。つらい。バブルプロットを使うのがテキスト通りの適切なアイディアです。一応載せておきます。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib.patches import Ellipse
from scipy import stats

def value_type(v):
    if v.unique().size < 5:
        v_type = "discrete"
    else:
        v_type = "continuous"
    return v_type


def correlation(x, y, **kws):
    r, _ = stats.spearmanr(x, y)
    ax = plt.gca()
    ax.axis('off')
    ellcolor = plt.cm.RdBu(0.5*(r+1))
    txtcolor = 'black' if np.absolute(r) < 0.5 else 'white'
    artist = Ellipse(xy=[.5, .5],
                     width=np.sqrt(1+r),
                     height=np.sqrt(1-r),
                     angle=45,
                     facecolor=ellcolor,
                     edgecolor='none',
                     transform=ax.transAxes)
    ax.add_artist(artist)
    ax.text(.5,
            .5,
            '{:.0f}'.format(r*100),
            color=txtcolor,
            fontsize=28,
            horizontalalignment='center',
            verticalalignment='center',
            transform=ax.transAxes)


def diagonal(x, **kws):
    ax = plt.gca()
    x_type = value_type(x)
    if x_type == "discrete":
        sns.countplot(x)
    else:
        sns.distplot(x, kde=False)


def distribution(x, y, **kws):
    ax = plt.gca()
    x_type = value_type(x)
    y_type = value_type(y)
    if x_type == "discrete":
        if y_type == "discrete":
            df = pd.DataFrame([x, y]).T
            df.columns=[x.name, y.name]
            pdf = df.pivot_table(index=x.name, columns=y.name, aggfunc=lambda x: len(x)).fillna(0).T
            plt.pcolor(pdf)
        else:
            sns.boxplot(x, y)
            sns.swarmplot(x, y)
    else:
        if y_type == "discrete":
            sns.boxplot(x, y, orient="h")
            sns.swarmplot(x, y, orient="h")
        else:
            plt.scatter(x, y)


def scatterplot_matrix(df):
    g = sns.PairGrid(df)
    g.map_upper(correlation)
    g.map_diag(diagonal)
    g.map_lower(distribution)
    return g

x = np.random.normal(100, 5, 30)
y = np.random.choice([1,2,3], 30, p=[0.1,0.2,0.7])
z = np.random.choice([1,2,3,4], 30, p=[0.4,0.3,0.2,0.1])
w = np.random.normal(4, 0.1, 30)
df = pd.DataFrame(np.array([x,y,z,w]).T, columns=["x", "y", "z", "w"])
g = scatterplot_matrix(df)
plt.show(g)

f:id:ajhjhaf:20170530195929p:plain

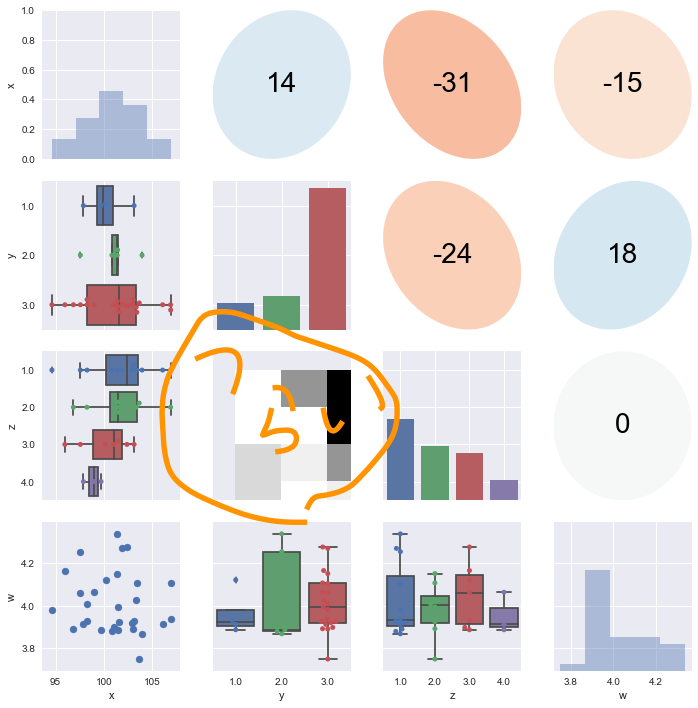
練習問題(1)

まぁほとんど弄る部分もありません。いつも通りPyStanを回すだけです。

import pystan
import pandas as pd
import os
import pickle
from IPython.core.display import display

stan_file = os.path.join("RStanBook", "chap05", "model", "model5-3.stan")
model = pystan.StanModel(stan_file)
    
df = pd.read_csv("./RStanBook/chap05/input/data-attendance-1.txt")
N = len(df)
A = df["A"].values
Score = df["Score"].values / 200
Y = df["Y"].values
stan_data = {
    "N": N,
    "A": A,
    "Score": Score,
    "Y": Y 
}
fit = model.sampling(
    data=stan_data,
    iter=2100,
    chains=4,
    warmup=100,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

mu = fit.extract()["mu"]
diff = np.apply_along_axis(lambda x: Y - x, axis=1, arr=mu)

モデルはgithubで公開されているものをそのまま使いました。

github.com

練習問題(2)

Stanの内部の生成量を出すところで残差を計算します。個人的には汚い部分を全部Stanの中に隠せるのでこっちのほうが好きです。

import pystan
import pandas as pd
import os
import pickle
from IPython.core.display import display

stan_file = os.path.join("RStanBook", "chap05", "model", "model5-3_kai.stan")
stan_file_c = os.path.join("RStanBook", "chap05", "model", "model5-3_kai.pkl")

# コンパイルチェック
if os.path.exists(stan_file_c) == False:
    # コンパイル済みのバイナリが無かったらstanファイルからコンパイル
    model = pystan.StanModel(stan_file)    
    with open(stan_file_c, "wb") as f:
        pickle.dump(model, f)
else:
    # バイナリがあったらそれを利用
    with open(stan_file_c, "rb") as f:
        model = pickle.load(f)
    
df = pd.read_csv("./RStanBook/chap05/input/data-attendance-1.txt")
N = len(df)
A = df["A"].values
Score = df["Score"].values / 200
Y = df["Y"].values
stan_data = {
    "N": N,
    "A": A,
    "Score": Score,
    "Y": Y 
}
fit = model.sampling(
    data=stan_data,
    iter=2100,
    chains=4,
    warmup=100,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

モデルは次の通りです。

data {
  int N;
  int<lower=0, upper=1> A[N];
  real<lower=0, upper=1> Score[N];
  real<lower=0, upper=1> Y[N];
}

parameters {
  real b1;
  real b2;
  real b3;
  real<lower=0> sigma;
}

transformed parameters {
  real mu[N];
  for (n in 1:N)
    mu[n] = b1 + b2*A[n] + b3*Score[n];
}

model {
  for (n in 1:N)
    Y[n] ~ normal(mu[n], sigma);
}

generated quantities {
  real y_pred[N];
  real diff[N] ;
  for (n in 1:N){
    y_pred[n] = normal_rng(mu[n], sigma) ;
    diff[n] = Y[n] - mu[n] ;
  }
}

つづいてpythonでグラフを描いて、目視で比較をします。

まず実測値とモデルによる予測値を比較してみます。テキストでは予測分布を使っていますが、試しにMCMCで推定されたパラメータ分布の中央値を使って値を予測してみます。この目的は、後述する事後予測分布との比較です。これは「はじめての統計データ分析」で言うところの、条件付き予測分布を使った手法です。こちらの手法だとStanファイル中で予測をしなくていい代わりに、エラーバーをつけるのがめんどくさいです。何故ならYを導出するための $\mu$ にも $\sigma$ にも分布があるので、その両方を考慮する必要があります。今回はパスさせて下さい。

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# Aの値でindexを分類する
A0_samples = df[df["A"] == 0].index
A1_samples = df[df["A"] == 1].index

# summaryのtableからmuの中央値とsigmaを取得する
summary_df_A0 = summary_df.loc[["mu[{0}]".format(i) for i in A0_samples], :]
summary_df_A1 = summary_df.loc[["mu[{0}]".format(i) for i in A1_samples], :]
map_A0 = summary_df_A0["50%"]
map_A1 = summary_df_A1["50%"]
sigma = summary_df.loc["sigma", "50%"]

# パラメータを使って条件付き予測分布を推定する
Y_A0 = Y[A0_samples]
Y_A1 = Y[A1_samples]
Y_A0A1 = np.hstack([Y_A0, Y_A1])
Y_ast_A0 = np.random.normal(map_A0, sigma)
Y_ast_A1 = np.random.normal(map_A1, sigma)
Y_ast_A0A1 = np.hstack([Y_ast_A0, Y_ast_A1])
# グラフのために相関係数を導出する
r = np.corrcoef(Y_A0A1, Y_ast_A0A1)[0][1]

# 可視化
fig, ax = plt.subplots()
ax.plot(Y_ast_A0, Y_A0, "o", label="A=0")
ax.plot(Y_ast_A1, Y_A1, "^", label="A=1")
ax.plot([0, 0.5], [0, 0.5], "k-")
ax.legend()

# 体裁を整える
ax.set_aspect('equal')
ax.set_xlabel("Predicted value(by EAP)")
ax.set_ylabel("Observed value")
ax.set_title("r={0}".format(r))
plt.show()

f:id:ajhjhaf:20170615161247p:plain

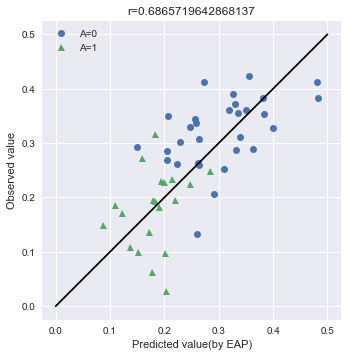
Aについてバラけているわけではないですが、あまり精度が良く無さそうです。モデルの精度が良くないのでしょうか(後述しますが、これは違います)?

続いて、MCMCサンプリングの中でyの予測値を推定します。これは「はじめての統計データ分析」で言うところの、事後予測分布を使った手法です。こちらのほうが分布全体を考慮して行っているので、正確な予測値を計算することが出来ます。エラーバーについてもMCMCの分布を使えばいいので簡単です。今回は教科書の80%区間ではなく、デフォルトで計算される75%区間を利用しています。

# Aの値でindexを分類する
A0_samples = df[df["A"] == 0].index
A1_samples = df[df["A"] == 1].index

Y_A0 = Y[A0_samples]
Y_A1 = Y[A1_samples]
Y_A0A1 = np.hstack([Y_A0, Y_A1])

# プロット点の計算
summary_df_A0 = summary_df.loc[["y_pred[{0}]".format(i) for i in A0_samples], :]
summary_df_A1 = summary_df.loc[["y_pred[{0}]".format(i) for i in A1_samples], :]
Y_pred_A0 = summary_df_A0["50%"]
Y_pred_A1 = summary_df_A1["50%"]
Y_pred = np.hstack([Y_pred_A0, Y_pred_A1])
# 誤差の計算
Y_pred_A0_err_down = (Y_pred_A0 - Y_pred_summary_A0["25%"]).values
Y_pred_A1_err_down = (Y_pred_A1 - Y_pred_summary_A1["25%"]).values
Y_pred_A0_err_up = (Y_pred_summary_A0["75%"] - Y_pred_A0).values
Y_pred_A1_err_up = (Y_pred_summary_A1["75%"] - Y_pred_A1).values
Y_pred_A0_err = np.vstack([Y_pred_A0_err_down, Y_pred_A0_err_up])
Y_pred_A1_err = np.vstack([Y_pred_A1_err_down, Y_pred_A1_err_up])
# 相関係数の計算
r = np.corrcoef(Y_A0A1, Y_pred)[0][1]

# 可視化
fig, ax = plt.subplots()
ax.errorbar(Y_pred_A0, Y_A0, yerr=Y_pred_A0_err, fmt="o", label="A=0")
ax.errorbar(Y_pred_A1, Y_A1, yerr=Y_pred_A1_err, fmt="^", label="A=1")
# y=xの線を書く
ax.plot([0, 0.5], [0, 0.5], "k-")
# 凡例をつける
ax.legend()

# 体裁を整える
ax.set_aspect('equal')
ax.set_xlabel("Predicted value")
ax.set_ylabel("Observed value")
ax.set_title("r={0}".format(r))
plt.show()

f:id:ajhjhaf:20170615161515p:plain

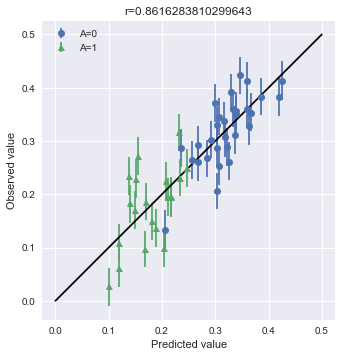
結果がわりと異なります。相関係数に如実に現れました。条件付き予測分布ではダメかと思ったモデルですが、こちらでは問題がなさげなことが推定されます。以上のことから、条件付き予測分布はオンラインで利用できるなどの利点がありますが、その分結果の浮動性があることを頭に入れたほうが良いと思います。とはいえ、どちらの方法でもAに関する偏ったバラつきが無いことはわかりますので、何を見たいかの使い分けが結局のところ肝心です。

最後に実測値とパラメータ $\mu$ の誤差を調べます。

summary_df_diff = summary_df.loc[["diff[{0}]".format(i) for i in range(0, 50)], :]

fig, ax = plt.subplots()
sns.distplot(summary_df_diff["50%"], bins=np.arange(-0.15, 0.15, 0.03), ax=ax)
ax.set_xlabel("Epsilon EAP")
ax.set_ylabel("Count")
plt.show()

f:id:ajhjhaf:20170615164959p:plain

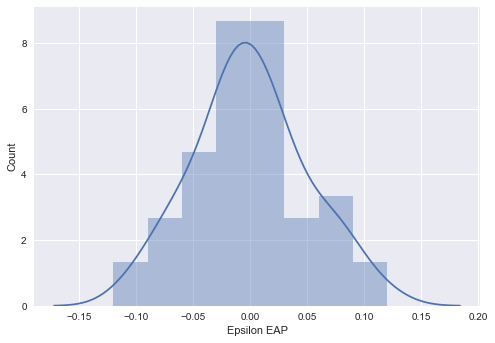
教科書の結果から分かっていましたが、きちんとあてはめた正規分布に従っています。

練習問題(3)

離散値と離散値の集計です。pandasのpivot_tableメソッドを使えばいいのですが、芸がないのでヒートマップで可視化しておきます。AとYの各組み合わせで足していけばいいので、ラムダ式を読み出してlenでカウントしました。

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

df = pd.read_csv("./RStanBook/chap05/input/data-attendance-3.txt")
pdf = df[["A", "Y"]].pivot_table(index="A", columns="Y", aggfunc=lambda x:len(x))
g = sns.heatmap(pdf, annot=True)
plt.show(g)

f:id:ajhjhaf:20170615170145p:plain

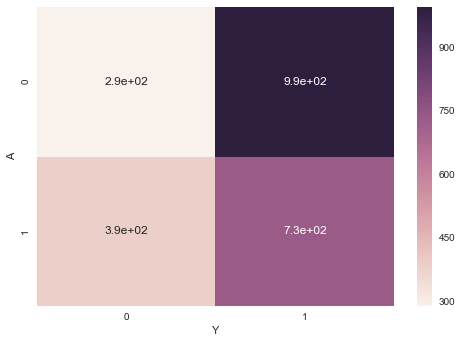
練習問題(4)

晴れがもたらす影響を基準値として、曇と雨が持つ影響についてもMCMCから推定してみます。これだけだと芸が無いので、WAICによるモデルのフィッティングについても評価してみます。

import pystan
import pandas as pd
import os
import pickle
import numpy as np
from IPython.core.display import display
from logging import getLogger, Formatter, StreamHandler, DEBUG

# printではなくloggerを使う
def get_logger():
    logger = getLogger(__name__)
    logger.setLevel(DEBUG)
    log_fmt = '%(asctime)s : %(name)s : %(levelname)s : %(message)s'
    formatter = Formatter(log_fmt)
    stream_handler = StreamHandler()
    stream_handler.setLevel(DEBUG)
    stream_handler.setFormatter(formatter)
    logger.addHandler(stream_handler)
    return logger
logger = get_logger()

stan_file = os.path.join("RStanBook", "chap05", "model", "model5-5_kai.stan")
model = pystan.StanModel(stan_file)    
    
trans = {"A": 1, "B": 2, "C": 3}
df = pd.read_csv("./RStanBook/chap05/input/data-attendance-3.txt")
I = len(df)
A = df["A"].values
Score = df["Score"].values / 200
W = df["Weather"].values
W = np.array([trans[w] for w in W])
Y = df["Y"].values
stan_data = {
    "I": I,
    "A": A,
    "Score": Score,
    "W": W,
    "Y": Y 
}
fit = model.sampling(
    data=stan_data,
    iter=1200,
    chains=4,
    warmup=200,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

log_lik = fit.extract("log_lik")["log_lik"]
waic = -2 * np.sum(np.log(np.mean(np.exp(log_lik), axis=0))) + 2 * np.sum(np.var(log_lik, axis=0))
logger.info("WAICの値は{0}です".format(waic))

モデルは以下の通りです。

data {
    int I;
    int<lower=0, upper=1> A[I];
    real<lower=0, upper=1> Score[I];
    int<lower=1, upper=3> W[I];
    int<lower=0, upper=1> Y[I];
}

parameters {
    real b[3];
    real b_w[2] ;
}

transformed parameters {
    real q[I];
    real beta_w[3] ;
    beta_w[1] = 0 ;
    beta_w[2] = b_w[1] ;
    beta_w[3] = b_w[2] ;

    for (i in 1:I)
        q[i] = inv_logit(b[1] + b[2]*A[i] + b[3]*Score[i] + beta_w[W[i]]);
}

model {
    for (i in 1:I)
        Y[i] ~ bernoulli(q[i]);
}

generated quantities {
    real log_lik[I] ;

    for (i in 1:I){
        log_lik[i] = bernoulli_lpmf(Y[i]|q[i]) ;
    }
}

さて経験的にパラメータを決定した時と比べて、WAICはどうなったでしょうか。

経験的に決めた場合 : WAIC=2769
MCMCからサンプリングした場合: WAIC=2764

ちょっとだけ、MCMCからサンプリングした場合のほうが値が良くなります。EAPを見てモデルを書いてみると

経験的に決めた場合

$Y \sim Bernoulli(q)$

$q = \frac{1}{1 + \frac{1}{exp(0.17 - 0.62 * A + 1.95 * Score - 0.45 * Weather)}}$

f:id:ajhjhaf:20170606192239p:plain:w200

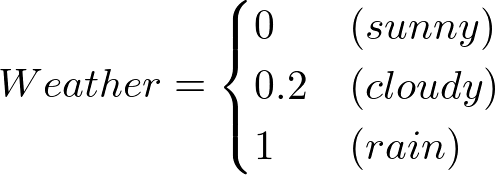
MCMCからサンプリングした場合

$Y \sim Bernoulli(q)$

$q = \frac{1}{1 + \frac{1}{exp(0.26 - 0.62 * A + 1.98 * Score + Weather)}}$

f:id:ajhjhaf:20170606192250p:plain:w200

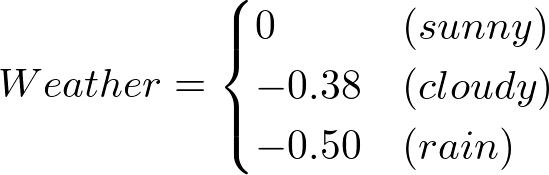
となります。Weatherの部分も係数の-0.45を考慮すると、そこまで変わりません。僕は経験的に得られた0:0.2:1が結構いいものであったと解釈しました。

つづいてpythonでグラフを描いて、目視で結果を比較します。テキストに描いてあるように、ロジスティック回帰の観測値は0/1になるので、可視化が難しいところです。qの値が、データからどのように変化するかを調べます。テキストの例では連続値のScoreと離散値のAが可視化されています。

まずScoreの影響を可視化します。

推測したqの中央値をデータと対応付けるために、indexを振り直します。
カラムを複数使ったデータの選択なので、queryメソッドで取得します。
qの中央値の線をきれいに書くためにソートを挟んでいます

# qの値を取得
summary_df_q = summary_df.loc[["q[{0}]".format(i) for i in range(0, I)], :]
q_range = summary_df_q[["25%", "50%", "75%"]]
q_range.index = range(len(q_eap))
# データと結合(順番はこの時点では保存されている)
df_concat = pd.concat([df, q_range], axis=1)
# 一部のデータだけ選択
df_filtered = df_concat.query("A == 0 & Weather == 'A'")
df_filtered = df_filtered.sort_values("Score")

# Yの点の位置をそれぞれちょっとずらす
y_randomized = [y + np.random.normal(0, 0.05) for y in df_filtered["Y"]]

# 可視化
fig, ax = plt.subplots()
ax.plot(df_concat_filtered["Score"], df_concat_filtered["50%"], "k-")
ax.fill_between(df_concat_filtered["Score"], df_concat_filtered["25%"], df_concat_filtered["75%"], facecolor="pink")
ax.plot(df_concat_filtered["Score"], y_randomized, "o", label="Y")
ax.legend()
ax.set_xlabel("Score")
ax.set_ylabel("q")
plt.show()

f:id:ajhjhaf:20170615181717p:plain

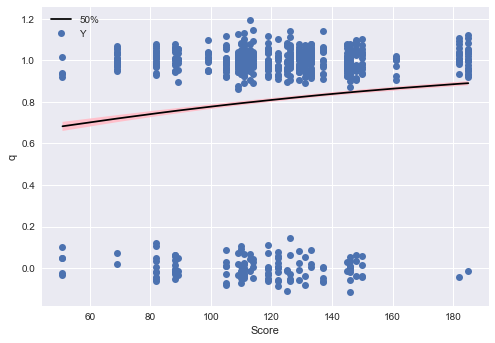
次にAに対するプロットを書きましょう。matplotlibで頑張るのが面倒だったのでseabornで書きました(なんかごめんなさい)。適材適所です！

# qの値を取得
summary_df_q = summary_df.loc[["q[{0}]".format(i) for i in range(0, I)], :]
q_range = summary_df_q[["25%", "50%", "75%"]]
q_range.index = range(len(q_eap))
# データと結合(順番はこの時点では保存されている)
df_concat = pd.concat([df, q_range], axis=1)

# 可視化
fig, ax = plt.subplots()
sns.violinplot(data=df_concat, x="50%", y="Y", ax=ax, orient="h")
sns.swarmplot(data=df_concat, x="50%", y="Y", hue="A", ax=ax, orient="h", palette=sns.color_palette("Set2", n_colors=2))
ax.set_xlabel("q")
ax.set_ylabel("Y")
plt.show()

f:id:ajhjhaf:20170615183431p:plain

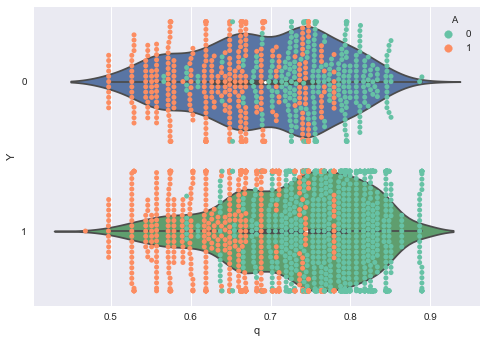
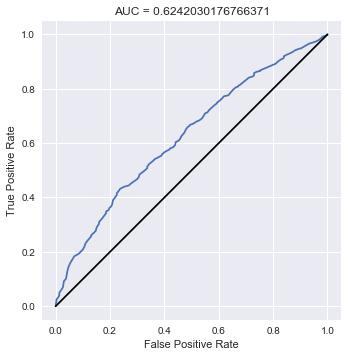
最後にROCカーブを書いて、AUCを計算します。これについてはScikit-learnを使うのが簡単でしょう。

from sklearn.metrics import roc_curve, roc_auc_score

summary_df_q = summary_df.loc[["q[{0}]".format(i) for i in range(0, I)], :]
q = summary_df_q["50%"]

# AUCの計算
auc = roc_auc_score(Y, q)

# ROCカーブの座標を計算
false_positive_rate, true_positive_rate, _ = roc_curve(Y, q)
fig, ax = plt.subplots()
ax.plot(false_positive_rate, true_positive_rate)
# y=xを描く
ax.plot([0, 1], [0, 1], "k-")

# 体裁を整える
ax.set_aspect('equal')
ax.set_xlabel("False Positive Rate")
ax.set_ylabel("True Positive Rate")
ax.set_title("AUC = {0}".format(auc))
plt.show()

f:id:ajhjhaf:20170615184747p:plain

練習問題(5)

import matplotlib.pyplot as plt
import os
import pandas as pd
import pickle
import pystan
from IPython.core.display import display

stan_file = os.path.join("RStanBook", "chap05", "model", "model5-6b.stan")
model = pystan.StanModel(stan_file)    
    
trans = {"A": 1, "B": 2, "C": 3}
df = pd.read_csv("./RStanBook/chap05/input/data-attendance-2.txt")
N = len(df)
A = df["A"].values
Score = df["Score"].values / 200
M = df["M"].values
stan_data = {
    "N": N,
    "A": A,
    "Score": Score,
    "M": M 
}
fit = model.sampling(
    data=stan_data,
    iter=2100,
    chains=4,
    warmup=100,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

Mpred = np.median(fit.extract()["m_pred"], axis=0)
fig = plt.figure(figsize=(5,5))
ax = fig.gca()
ax.plot(Mpred, M, "o")
ax.plot(range(0, 100), range(0, 100))
ax.set_xlim(0, 100)
ax.set_ylim(0, 100)
ax.set_xlabel("Predicted")
ax.set_ylabel("Measured")

plt.show(ax)

f:id:ajhjhaf:20170615184732p:plain

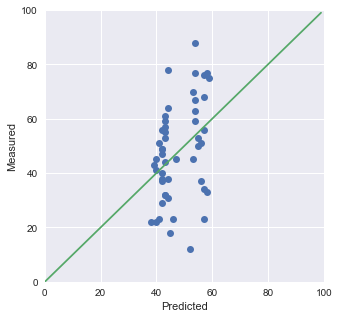
全然y=xに乗っていません…(合っているのかめちゃめちゃ不安です)。

この結果からは、予測が出来ていないことが分かります。説明変数が足りてないということですね。よくあることですが、計測が終わった後にこうなった場合は、新しくメタデータを足して計測し直しになるわけです。つらい。

練習問題(6)

練習問題(5)と(6)はちょっと気をつける必要があります。アヒル本だけ読んだ時には「処理」の違いというものが

両方に別々の処理を施した
片方には処理を施して、片方には何もしなかった

という2つのパターンのどちらなのか分かりません。前者の場合にはベースラインとなるものに別々の効果が生じることを予測できますが、後者の場合には一方だけはベースラインのままで、もう一方に何か効果が現れることになります。

データの元となった緑本を読んでみると、後者であることが分かります。前者を踏まえてモデルを作ってみると、MCMCが収束せずに頭を悩まるハメになります(僕は緑本を読んだはずなのに忘れていて喘ぎました)。

前者の場合でも相対的な効果を踏まえると同じじゃないの？と思っていたのですが収束しないですし、そうではないんですね。ちょっとした発見でした。これはChapter 10の一番初めに出てくる識別可能性の問題に引っかかるからですね。

import pystan
import pandas as pd
import os
import pickle
from IPython.core.display import display

stan_file = os.path.join("RStanBook", "chap05", "model", "practice6.stan")
model = pystan.StanModel(stan_file)    
    
trans = {"C": 0, "T": 1}
df = pd.read_csv("./RStanBook/chap05/input/data3a.csv")
N = len(df)
X = df["x"].values
F = df["f"].values
F = np.array([trans[x] for x in F])
Y = df["y"].values
stan_data = {
    "N": N,
    "X": X,
    "F": F,
    "Y": Y 
}
fit = model.sampling(
    data=stan_data,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

モデルは次です。

data {
    int N;
    real<lower=0> X[N];
    int<lower=0, upper=1> F[N];
    int<lower=0> Y[N];
}

parameters {
    real b[3] ;
}

transformed parameters {
    real<lower=0> lambda[N] ;

    for (n in 1:N){
        lambda[n] = exp(b[1] + b[2]*X[n] + b[3] * F[n]) ;
    }
}

model {
    for (n in 1:N){
        Y[n] ~ poisson(lambda[n]);
    }
}

練習問題(7)

(6)と同様に処理の効果にだけ気をつけて下さい。

import pystan
import pandas as pd
import os
import pickle
from IPython.core.display import display

stan_file = os.path.join("RStanBook", "chap05", "model", "practice7.stan")
model = pystan.StanModel(stan_file)    
    
trans = {"C": 0, "T": 1}
df = pd.read_csv("./RStanBook/chap05/input/data4a.csv")
I = len(df)
N = df["N"].values
X = df["x"].values
F = df["f"].values
F = np.array([trans[x] for x in F])
Y = df["y"].values
stan_data = {
    "I": I,
    "N": N,
    "X": X,
    "F": F,
    "Y": Y 
}
fit = model.sampling(
    data=stan_data,
    iter=1500,
    chains=4,
    warmup=500,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

モデルは以下の通りです。

data {
    int I;
    int<lower=0> N[I];
    real<lower=0> X[I];
    int<lower=0, upper=1> F[I];
    int<lower=0> Y[I];
}

parameters {
    real b[3] ;
}

transformed parameters {
    real<lower=0> q[I] ;

    for (i in 1:I){
        q[i] = inv_logit(b[1] + b[2]*X[i] + b[3]*F[i]) ;
    }
}

model {
    for (i in 1:I){
        Y[i] ~ binomial(N[i], q[i]) ;
    }
}

練習問題(4), (6)と(7)は初めに取り組んだ時に、モデルが全然収束しなくて足踏みしました。そういう時にはMCMCサンプリングが無理をして変な部分を探索しようとするのでめちゃめちゃ時間がかかります。なので待機時間で「失敗したな」と悟れたりするのはちょっと面白いところです。

index	week	arrest	fin	age	race	wexp	mar	paro	prio
0	20	1	0	27	1	0	0	1	3
1	17	1	0	18	1	0	0	1	8
2	25	1	0	19	0	1	0	1	13
3	52	0	1	23	1	1	1	1	1
4	52	0	0	19	0	1	0	1	3
5	52	0	0	24	1	1	0	0	2
6	23	1	0	25	1	1	1	1	0
7	52	0	1	21	1	1	0	1	4
8	52	0	0	22	1	0	0	0	6
9	52	0	0	20	1	1	0	0	0
10	52	0	1	26	1	0	0	1	3

index	week	arrest	fin	age	race	wexp	mar	paro	prio
0	20	1	0	27	1	0	0	1	3
1	17	1	0	18	1	0	0	1	8
2	25	1	0	19	0	1	0	1	13
3	52	0	1	23	1	1	1	1	1
4	52	0	0	19	0	1	0	1	3
5	52	0	0	24	1	1	0	0	2
6	23	1	0	25	1	1	1	1	0
7	52	0	1	21	1	1	0	1	4
8	52	0	0	22	1	0	0	0	6
9	52	0	0	20	1	1	0	0	0
10	52	0	1	26	1	0	0	1	3

index	week	arrest	fin	age	race	wexp	mar	paro	prio
0	20	1	0	27	1	0	0	1	3
1	17	1	0	18	1	0	0	1	8
2	25	1	0	19	0	1	0	1	13
3	52	0	1	23	1	1	1	1	1
4	52	0	0	19	0	1	0	1	3
5	52	0	0	24	1	1	0	0	2
6	23	1	0	25	1	1	1	1	0
7	52	0	1	21	1	1	0	1	4
8	52	0	0	22	1	0	0	0	6
9	52	0	0	20	1	1	0	0	0
10	52	0	1	26	1	0	0	1	3