概要

この記事はStanアドベントカレンダー-5日目の記事です(冗談です)。趣味でやっている円周分布の勉強もそこそこ進みました。この記事では、清水本に載っている逆Batchelet変換(Inverse batschelet transformation)を使った分布をStanで実装して、現時点での問題点について考察します。

角度データのモデリング (ISMシリーズ:進化する統計数理)

作者: 清水邦夫
出版社/メーカー: 近代科学社
発売日: 2018/01/30
メディア: 単行本
この商品を含むブログ (1件) を見る

背景

円周分布として有名なものとして、von Mises分布、心臓分布、巻き込みコーシー分布などがあります。しかしこれはいずれも平均パラメータで最頻値(=モード)を取り、その左右に集中度パラメータに応じた分散が対称に存在する分布です。しかし実際のデータでは、どちらかの方向に分散が偏ることがあります。このような非対称分布の拡張は円周分布のみならず、正規分布などでも考察されています。日本語資料でしたら豊田黄色本などに記述があります。

実践ベイズモデリング -解析技法と認知モデル-

作者: 豊田秀樹
出版社/メーカー: 朝倉書店
発売日: 2017/01/25
メディア: 単行本（ソフトカバー）
この商品を含むブログ (2件) を見る

さて円周分布では、次のような拡張があります。

Sine-skewed distirbution

清水本の中では、非対称な円周分布を構築する方法の一つとして正弦確率摂動法によるSine-skewed分布が載せられています。原著論文は(Abe, 2011)です。

link.springer.com

この分布は確率密度関数の設計が簡単なので、推定が容易というメリットがあります。更に確率密度関数の全区間の積分値である $\int_{-\pi}^{\pi}p(\theta)d\theta = 1$ という式が保持され、正規化が不要です。その一方で分散が集中度パラメータ(concentration parameter)だけでは制御されず、歪度パラメータからも影響を受けてしまう欠点があります。

Batschelet transformation

一方で、もともと円周分布を歪ませる方法としては(Batschelet, 1981)で提案された方法が有名です。

この方法では、 $vonmises(\theta|\mu, \kappa)$ を基に、 $aevonmises(\theta | \mu, \kappa, \nu) = vonmises(\theta + \nu\cos(\theta - \mu) | \mu, \kappa)$ と変換を加えます。この方法は分かりやすいし簡単なのですが、 $\int_{-\pi}^{\pi}aevonmises(\theta|\mu, \kappa, \nu) d\theta = 1$ が維持されません。そのためvon Mises分布とは確率密度関数の形がやや変わり、 $aevonmises(\theta|\mu, \kappa, \nu) = \frac{\exp(\kappa(\cos(\theta - \mu + \nu\cos(\theta - \mu)))}{c_{\mu, \kappa, \nu}}$ となります。 $c_{\mu, \kappa, \nu}$ は正規化定数で、 $c_{\mu, \kappa, \nu} = \int_{-\pi}^{\pi} \exp(\kappa(\cos(\theta - \mu + \nu\cos(\theta - \mu)))$ により求められます。確率密度関数の和が1となるように、全区間で積分して和を取り、割るという至極単純なアイディアです。

しかしこの計算は積分が入って面倒です。この記事では扱いませんが、現時点ではStanに積分機能が無いので、合成シンプソン法などの数値計算で代替するのが一つのアイディアになります。なお(Batschelet, 1981)は絶版になり手に入りませんが、(Abe, 2013)でより一般的に拡張されて説明されてますので、そちらを参考にすると良いかと思います。

link.springer.com

Inverse Batschelet transformation

(Jones&Pewsey, 2012)では、逆変換 $s(\theta) = t^{-1}_{1, \nu}(\theta)$ をかませることで、正規化が不要な非対称分布を作りました。 $t^{-1}_{1, \nu}(\theta)$ は $t_{1, \nu}(\theta) = \theta -\mu - \nu(1 + \cos(\theta-\mu)$ の逆関数です。s(t)は閉型(closed-form)で、つまり簡単な形で表すことが出来ません。このような逆関数の変換を含んだ分布の例を殆ど見ないので、これを実装してみます。参考とした論文は(Jones&Pewsey, 2012)と、Pewseyらの書いた"Circular statistics in R"です。

Circular Statistics in R

作者: Arthur Pewsey,Markus Neuhauser,Graeme D. Ruxton
出版社/メーカー: Oxford University Press, Usa
発売日: 2014/01/01
メディア: ペーパーバック
この商品を含むブログ (4件) を見る

結果

例によってpythonです。Rの本を見てるのに…。　

逆変換で知りたい値は既知の $t, \mu, \kappa, \nu$ のもとで $t = \theta -\mu - \nu(1+\cos(\theta - \mu))$ を満たすような $\theta$ です。観測値= $t$ が既知ということがポイントです。この場合には $g(\theta) = -t + \theta -\mu - \nu(1+\cos(\theta - \mu))$ という関数を考えて、 $g(\theta) = 0$ となるような $\theta$ を求めます。どちらにせよ非線形な問題ですが、0となる値を求めるには効率的なアルゴリズムがあるので、それを利用することができます(Wikipediaにもそんな記載があります)。3つの手法を紹介します。

シミュレーションデータは次のように作成しました。歪度パラメータが0である場合、通常のvon Mises分布と一致しますので、きちんと0が推定されるか調べます。

I = 1000
RADIAN = vonmises.rvs(size=I, loc=0, kappa=1.0)
stan_data = {
    "I": I,
    "RADIAN": RADIAN
}

Stanの組み込み関数を利用する

StanのVersion 2.17.0以降には、algebra_solverという関数で、非線形方程式の場合にも解を得ることができます。この関数はPowell法を使っています(Powell, 1970)。Stanコードの実装は次のとおりです。

1~17, 48行目: 逆変換をする処理です。
24~33行目: algebra_solverへ投入するデータを宣言しています。

algebra_solverはStanのマニュアルの20節に記述があります。第1引数へ解を求める関数、第2引数へその際の解、第3引数へパラメータ、第4引数へ実数型の定数値、第5引数へ整数型の定数値を使います。ちょっと使い方にはコツがあります。

先程も書きましたが、今回の場合は観測値= $t$ が既知ということがポイントです。これがパラメータになりますので、第3引数へ入れます。
その他モデル上でのパラメータ $\mu, \nu$ などもパラメータです。普通のプログラミング言語ではkargsなんかを使うのですが、第3引数にはvector型しか受け付けないので、観測値の長さより少し伸ばして代入します。
定数値は今回の場合、観測値の長さしかありません。これは整数型です。実数型に該当するものは無いのですが、宣言は必要なので長さ0のベクターをtransformed_dataのブロックで宣言しておきます。

性能評価してみましょう。サンプルサイズを変えてデータを何回か生成し、真の分布に対するKL divergenceを調べます。

result = []
for I in [100, 300, 500, 1000]:
    for i in range(5):
        RADIAN = vonmises.rvs(size=I, loc=0, kappa=1.0)
        stan_data = {
            "I": I,
            "RADIAN": RADIAN
        }

        fit = model.optimizing(stan_data, init_alpha=1e-10)
        p = invBvonmises_pdf(theta, kappa=fit["kappa"], nu=fit["nu"], loc=fit["mu"])
        pt = invBvonmises_pdf(theta, kappa=1.0, nu=0, loc=0)
        kld = entropy(p, pt)
        tmp = {"I": I, "i": i, "kld": kld}
        result.append(tmp)
df = pd.DataFrame(result)

fig = plt.figure()
ax = fig.add_subplot(111)
sns.boxplot(data=df, x="I", y="kld", ax=ax)
ax.set_xlabel("Sample size")

f:id:ajhjhaf:20181126092909p:plain

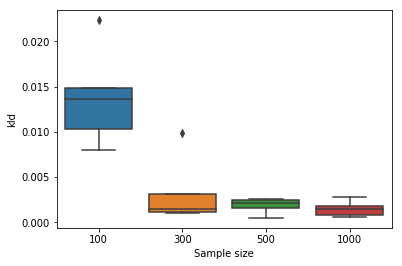
データ量に応じてきちんと真の分布との距離が小さくなっていることがわかります。

ニュートン法

組み込み関数は目的関数だけあれば使える便利な手法ですが、めちゃめちゃ遅いです。ベクトル形式で渡していますが、データ数がある程度あるとほとんど使い物になりません。I=500の時点で、平均11秒ほどかかります。今回の実験がMCMCではなく、MAP推定で実行しているのもそれが理由となります。幸いにも、今回の変換は微分可能な形式で示されていますので、傾きの情報を利用したニュートン法が一つのアイディアとして考えられます。この場合には解が二次収束しますので、非常に早く計算可能です。Stanのコードは次のとおりです。

1~23, 38行目: ニュートン法での逆変換です。
- 8行目: 初期値として、 $\theta$ の値を使います。色々試したが、この関数の場合はこれが安定的でした。
- 9行目: $g(\theta)$ を評価します。これがすべて0なら理想形です。
- 10行目: 絶対値を取って、どれだけ0に近付ているか評価します。
- 11行目: 反復回数の上限値を決めます。これを決めておかないと、何かあって0に近づかなかった場合は無限に計算されてしまいます。
- 12行目: どれだけ0に近づいたら終了するか決めます。Stanの場合はmachine_precision()が計算機イプシロンとして用意されていますので、これを使います。
- 13~15行目: tを傾きを使って更新して、誤差を再評価します。12行目で決めた基準より小さくなったら終了です。
- 16~19行目: 反復回数が上限に達したら、反復を強制的に終了します。

先ほどと同様の誤差計算は次のとおりになります。こちらでも、問題なくKL divergenceが0に近づいています。

f:id:ajhjhaf:20181126094621p:plain

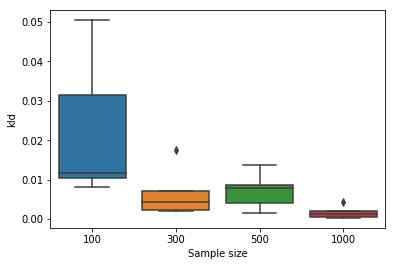
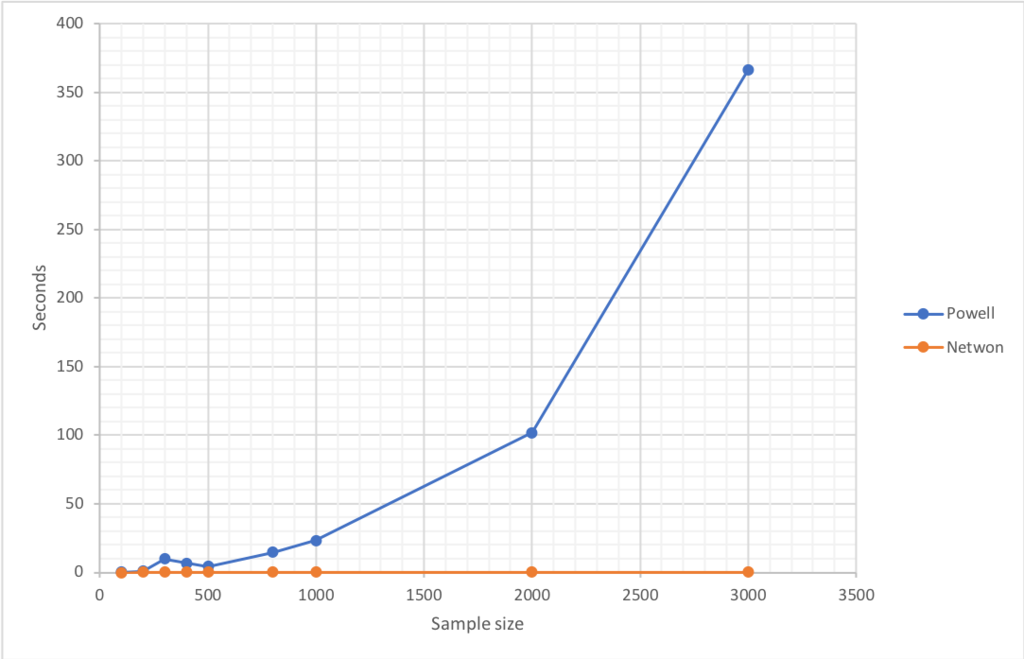
肝心の速度についてもI=500の段階で0.1秒と100倍ほど高速化することができました。2つの手法を比較すると、次のとおりになります。Powellが指数増加していることがわかります。

f:id:ajhjhaf:20181126094802p:plain

二分法

ニュートン法でハッピーエンドを迎えられるかと思いきや、そうはなりません。RstanにはStanの関数を呼び出すexpose機能があります。 $s(t)$ がどのような挙動をするか調べてみましょう。先程のモデルを適当に保存してください。

library("rstan")
rstan::expose_stan_functions("Desktop/invBvonmises.stan")
x = seq(-pi, pi, length=1000)
mu = 0
nu = 0.99
I = 1000
y = inv_transformation_Batschelet(x, mu, nu, I)
plot(x, y)

f:id:ajhjhaf:20181126095608p:plain

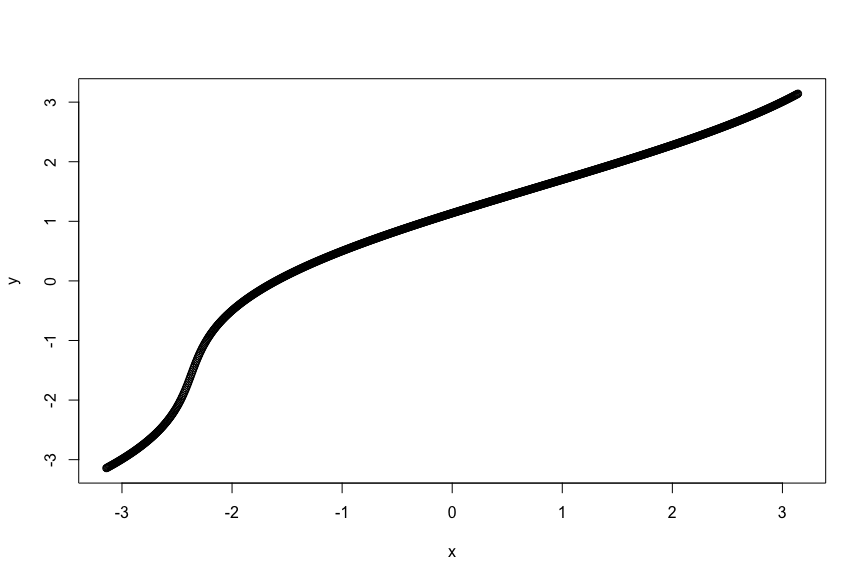
良さそうに見えます。が、ここでnuの値を極めて大きくしてみましょう。

f:id:ajhjhaf:20181126095532p:plain

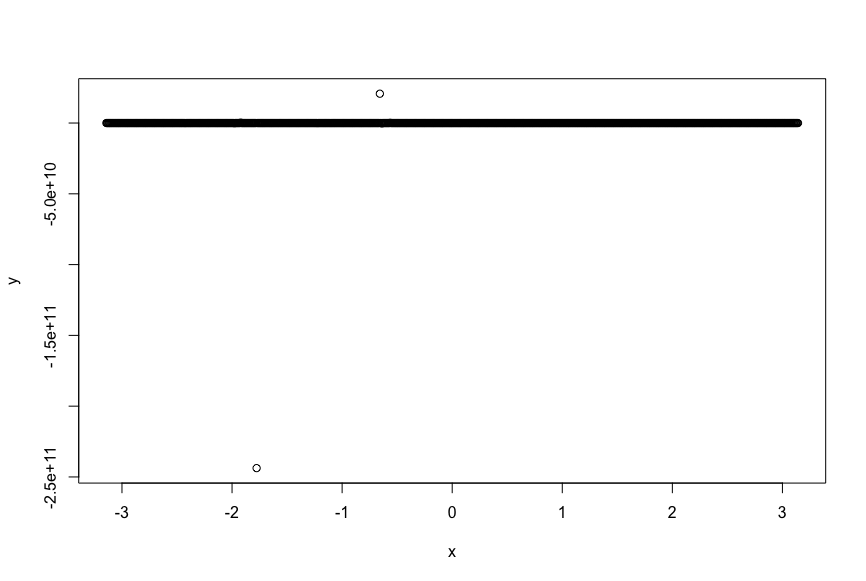
ぶっ壊れた値が出てきてしまいました。これは、 $\nu$ が大きい場合に、勾配が消失することが原因と思われます。 $g(\theta)$ を $\nu$ が大きい場合に書いてみますと、次のとおりです。

mu = 0
nu = 0.99
theta = 0
x = np.linspace(-np.pi, np.pi, 1000)
y = x - nu * (1 + np.cos(x - mu)) - theta

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y)
ax.set_xlabel("theta")
ax.set_ylabel("g(theta)")

f:id:ajhjhaf:20181126095943p:plain

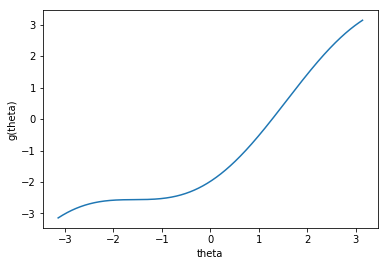
thetaが-2から-1の場合にかけて、勾配が消失していることが見て取れます。この場合には、傾きを使わない手法として、二分法を使うことが考えられます。Stanのモデルは次のとおりです。

1~34行目: 二分法による逆変換です。
- 10-11行目: 上界、下界を決めます。求める解の範囲が $-\pi$ から $\pi$ なので、それぞれ $g(\theta)$ が0以上、以下となるように決めましょう。
- 12行目: 上界、下界から真ん中の値をとります。
- 13-14行目: ニュートン法と同様に、 $g(\theta)$ の評価をして、誤差を調べます。
- 17-23行目: 評価値の正負に応じて、上界、下界を狭めます。pythonだったらnumpyのsmart indexを使えば一行でかけますが、Stanだとfor文で一つ一つ判定しなくてはいけません
- 28行目: 二分法は一次収束です。ニュートン法と同等の精度を得るために、1000(>30²)回を反復上限とします。

R側から呼び出して、同様に計算させてみると、変換できたことがわかります。

f:id:ajhjhaf:20181126104135p:plain

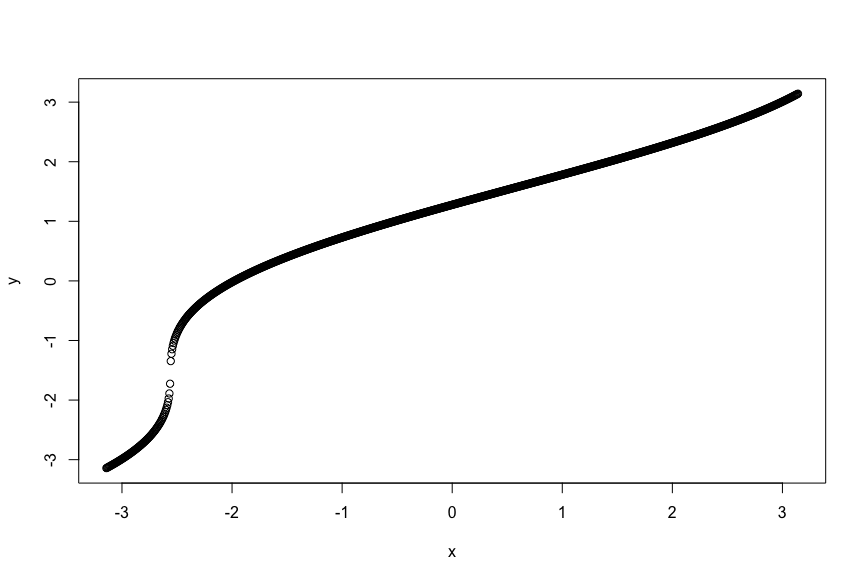
が、ここで大きな問題があります。R側での動作を見るに動きそうなこのモデルですが、実際に動かしてみるとLS failedが発生してうまくいきません。ナンデ……。大きな $\nu$ から作ったデータに対してフィッティングしてエラーが起こるなら、変換の勾配が消失して微分できず失敗すると納得できるのですが、ここまで使ってきた $\nu=0$ のデータに対して実行してもやはり失敗します。

まとめ

陽的に式をかけない変換を含むモデリングを実行することができました。Powell法だと(おそらく)数値的に安定なので使いやすいですが、データが多い場合には変換が非効率でめちゃめちゃ時間がかかります。ニュートン法は超絶早いですが、傾きがある場合じゃないと使えません。手元でまともに動く範囲を調べて、パラメータ制約つけるのがいいでしょうか…。二分法はなぜかうまくいきません。困った(ちなみにdiscourseで絶賛助けを求めています、コメント歓迎です……)。

今回利用したコードは、こちらにあります。再現実験したい方はどうぞ。

謝辞

このブログ記事を書くにあたり、StanのdiscourseでBen Bales氏に助けていただきました。お礼を申し上げます。

Easy to type

個人的な勉強の記録です。データ分析、可視化などをメイントピックとしています。

Stanで非閉型な逆関数を含む分布のモデリング

概要

背景

Sine-skewed distirbution

Batschelet transformation

Inverse Batschelet transformation

結果

Stanの組み込み関数を利用する

ニュートン法

二分法

まとめ

謝辞