StanとPythonでベイズ統計モデリング その2 Chapter5

アヒル本(StanとRでベイズ統計モデリング)のChapter5にPythonで取り組んでいきます。 練習問題を解いて、本文中に書かれてるグラフをPythonで描いてみます。

なおChapter1~3は導入だったのと、Chapter4は練習問題の内容が「はじめての統計データ分析」と被っていたのでパスします。

---

Chapter5 基礎的な回帰とモデルのチェック

• 重回帰
  • 複数の説明変数を用いた回帰のこと
    • 重回帰も結局は正規分布を仮定している
  • 目的
    • 説明変数からの応答変数の予想、及び説明変数の寄与率
  • 分布
    • 複数の説明変数ならScatterplot matrixを利用すると良い
  • MCMCの設定について
    • スケーリング: MCMCを行う前に、各データのオーダーを大体(1前後に)そろえること。
      • 収束がしやすく、早くなる
      • 最大値、標準偏差、標準偏差の倍で割ったりすれば良い
  • 結果の解釈 : モデルの改善に活かす!
    • 因果関係の推定
      • どちらが先に起こりうるか、といった事前知識が必要
    • 外挿
      • 利用したデータが の範囲であるにも関わらず、のようなデータをモデルに当てはめて予測することを外挿と呼ぶ。大体は予想外のデータなので、上手く行かない。
    • パラメータの幅
      • EAPなどの点推定量より、幅がどうなっているかが大事(0を跨いだりしていないか？)
    • 可視化
      • 実測値と予測値のプロット(データと予測分布)
        • X軸にデータ、Y軸にEAPから得られる予測値をプロット
        • y = xの直線から大きく外れることがなければOKとする
      • 推定ノイズの分布
        • ノイズの分布を仮定した時に、それがモデルに従っているか確認する
    • MCMCサンプルの散布図行列
      • パラメータの関係について読み取れる
• (二項)ロジスティック回帰
  • ロジスティック関数をつかった方法
    • 応答変数が0から1の間にある場合、説明変数に適用することで値の範囲を変換することが出来る
  • 2項分布モデル
    • 正規分布が当てはまらない場合には特に有効
    • 値が整数で幅が小さく、連続値とみなせないような場合に使う
    • Nが十分に大きい場合は正規分布に近似できる(正規分布の方が演算が高速なのでよい)
  • ベルヌーイ分布モデル
    • 応答変数がbool値であるような時にはベルヌーイ分布を利用すれば良い
  • 生成量
    • オッズ
      • 二項ロジスティック回帰モデルにおいて、であり、であるならばと変換することが出来る
      • はオッズと呼ばれる
      • その事象が起こるサンプリング確率の比率を示す
  • 可視化
    • ベルヌーイ分布を利用した場合
      • より推定されたqを利用する
      • 判断基準の閾値cを決定して、qとcからTP, FP, FN, TNの計算を行う
      • FP, TPを各qについてplotして曲線(ROC)を書く
      • ROCを下回った部分がAUCで、0.8以上だと良いものとされる
• ポアソン回帰
  • カウントデータに対して予測を行う時に用いる
    • でカウントデータYが決定されるものとして、は説明変数の線形結合を0以上に変換したものを使う(がよく使われる)
    • パフォーマンスの理由より、が十分に大きいなら、正規分布で近似して良い

練習問題

Scatterplot matrixについて

Pythonの実装はpandasマスターのid:sinhrksさんの記事を見るのが良いと思います。

sinhrks.hatenablog.com

個人的な使った感想は次の通りです。

• 離散値の可視化が上手く行かないことがある(6離散値指定したのに、4つしか表示されないことがある)？
  • たぶんこれはseabornのPairPlotのバグです……
  • 離散値/連続値判定の初期値が大きすぎると上手くいかないので、離散値の判定閾値を4, 5辺りにいじって使いました。
• 離散値の場合は対角のカウントはcountplotを使ったほうが良い？
  • 他の下半分、上半分のグラフと軸を合わせやすくするためです。
  • どうせseabornはPairGridで使うことになりますし…

そういうわけで改造させて頂いたバージョンがこちらです。残念ながら1つ目のバグは取れていません。そもそも僕の環境に特有なのかもしれませんし、諦めました。 上三角行列の部分はid:statmodelingさんの記事のまんまです。

statmodeling.hatenablog.com

#!/usr/bin/env python
# vim:fileencoding=utf-8
# Created: 2017-06-06
# Original scripts: http://sinhrks.hatenablog.com/entry/2016/11/01/075527

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib.patches import Ellipse


class Dispatcher(object):

    def __init__(self, fontsize=20, alpha=0.6, cmap='RdBu', threshold=5):
        self.fontsize = fontsize
        self.alpha = alpha
        self.cmap = plt.get_cmap(cmap)

        # 離散値 / 連続値とみなす閾値
        self.threshold = threshold

    def comb(self, x_series, y_series, label=None, color=None):
        """ 下三角部分のプロット """

        x_nunique = x_series.nunique()
        y_nunique = y_series.nunique()

        if x_nunique < self.threshold and y_nunique < self.threshold:
            # 離散値 x 離散値のプロット
            return self._dd_plot(x_series, y_series, label=label, color=color)

        elif x_nunique < self.threshold or y_nunique < self.threshold:
            # 離散値 x 連続値のプロット
            return self._dc_plot(x_series, y_series, label=label, color=color)

        else:
            # 連続値 x 連続値のプロット
            return plt.scatter(x_series, y_series, label=label, color=color)

    def _dd_plot(self, x_series, y_series, label=None, color=None):
        """ 離散値 x 離散値のプロット """

        # x, y 各組み合わせの個数を集計
        total = y_series.groupby([x_series, y_series]).count()

        # x, y軸をプロットする位置を取得
        xloc = total.index.labels[0]
        yloc = total.index.labels[1]
        values = total.values

        ax = plt.gca()
        for xp, yp, vp in zip(xloc, yloc, values):
            ax.annotate(vp,
                        (xp, yp),
                        fontsize=self.fontsize,
                        ha='center',
                        va='center')

        # 組み合わせの個数を散布図としてプロット
        size = values / (values.max() * 1.1) * 100 * 20
        ax.scatter(xloc, yloc, s=size, label=label, color=color)
        ax.set_ylim(yloc[0] - 0.5, yloc[-1] + 0.5)

    def _dc_plot(self, x_series, y_series, label=None, color=None):
        """ 離散値 x 連続値のプロット """

        if y_series.nunique() < x_series.nunique():
            # y軸が離散値の場合は、x, yを入替
            # 水平方向に箱ひげ図をプロット
            orient = "h" 
        else:
            orient = "v" 

        ax = sns.boxplot(x_series, y_series, orient=orient, color=color)
        ax = sns.swarmplot(x_series, y_series, orient=orient, color=color) 

    def diag(self, x_series, label=None, color=None):
        """ 対角部分のプロット """

        x_nunique = x_series.nunique()
        if x_nunique < self.threshold:
            ax = sns.countplot(x_series, color=color)
        else:
            ax = sns.distplot(x_series, kde=False, color=color)
        ax.yaxis.set_visible(False)

    def ellipse(self, x_series, y_series, label=None, color=None):
        """ 上三角部分のプロット """

        # 相関係数を楕円としてプロット
        r = x_series.corr(y_series)
        c = self.cmap(0.5 * (r + 1))
        ax = plt.gca()
        ax.axis('off')
        artist = Ellipse(xy=[.5, .5],
                         width=np.sqrt(1+r),
                         height=np.sqrt(1-r),
                         angle=45,
                         facecolor=c,
                         edgecolor='none',
                         transform=ax.transAxes)
        ax.add_artist(artist)
        ax.text(.5,
                .5,
                '{:.0f}'.format(r*100),
                fontsize=28,
                horizontalalignment='center',
                verticalalignment='center',
                transform=ax.transAxes)

       
d = Dispatcher()

# データを作る
x = np.random.normal(100, 5, 30)
y = np.random.choice([1,2,3], 30, p=[0.1,0.2,0.7])
z = np.random.choice([1,2,3,4], 30, p=[0.2,0.2,0.2,0.4])
w = np.random.normal(4, 0.1, 30)
df = pd.DataFrame(np.array([x,y,z,w]).T, columns=["x", "y", "z", "w"])

# 可視化する
g = sns.PairGrid(df, diag_sharey=False)
g.map_diag(d.diag)
g.map_lower(d.comb)
g.map_upper(d.ellipse)
plt.show()

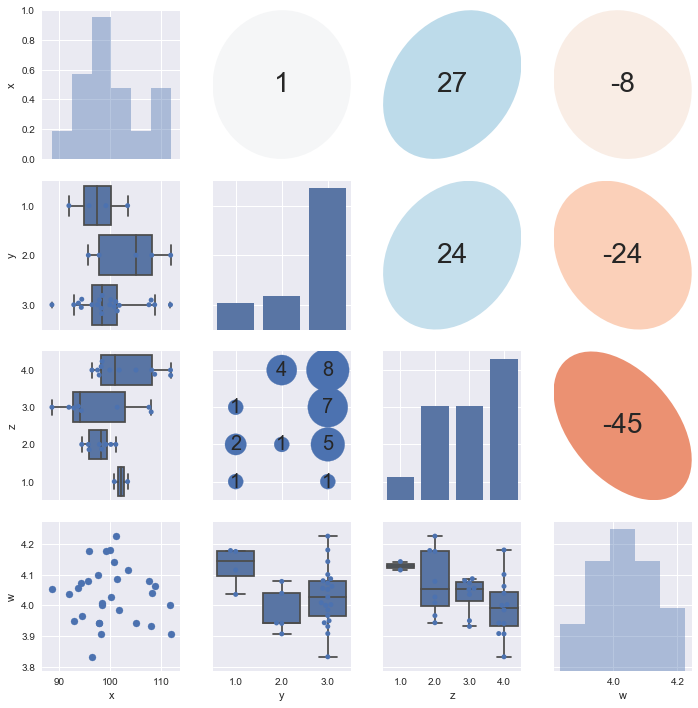
これとは別に、勉強として自分でも実装してみましたが、離散×離散の可視化が難しいところです。僕はヒートマップを使おうかと思ったのですが、軸を表示しようとする関係でズレます。つらい。バブルプロットを使うのがテキスト通りの適切なアイディアです。 一応載せておきます。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib.patches import Ellipse
from scipy import stats

def value_type(v):
    if v.unique().size < 5:
        v_type = "discrete"
    else:
        v_type = "continuous"
    return v_type


def correlation(x, y, **kws):
    r, _ = stats.spearmanr(x, y)
    ax = plt.gca()
    ax.axis('off')
    ellcolor = plt.cm.RdBu(0.5*(r+1))
    txtcolor = 'black' if np.absolute(r) < 0.5 else 'white'
    artist = Ellipse(xy=[.5, .5],
                     width=np.sqrt(1+r),
                     height=np.sqrt(1-r),
                     angle=45,
                     facecolor=ellcolor,
                     edgecolor='none',
                     transform=ax.transAxes)
    ax.add_artist(artist)
    ax.text(.5,
            .5,
            '{:.0f}'.format(r*100),
            color=txtcolor,
            fontsize=28,
            horizontalalignment='center',
            verticalalignment='center',
            transform=ax.transAxes)


def diagonal(x, **kws):
    ax = plt.gca()
    x_type = value_type(x)
    if x_type == "discrete":
        sns.countplot(x)
    else:
        sns.distplot(x, kde=False)


def distribution(x, y, **kws):
    ax = plt.gca()
    x_type = value_type(x)
    y_type = value_type(y)
    if x_type == "discrete":
        if y_type == "discrete":
            df = pd.DataFrame([x, y]).T
            df.columns=[x.name, y.name]
            pdf = df.pivot_table(index=x.name, columns=y.name, aggfunc=lambda x: len(x)).fillna(0).T
            plt.pcolor(pdf)
        else:
            sns.boxplot(x, y)
            sns.swarmplot(x, y)
    else:
        if y_type == "discrete":
            sns.boxplot(x, y, orient="h")
            sns.swarmplot(x, y, orient="h")
        else:
            plt.scatter(x, y)


def scatterplot_matrix(df):
    g = sns.PairGrid(df)
    g.map_upper(correlation)
    g.map_diag(diagonal)
    g.map_lower(distribution)
    return g

x = np.random.normal(100, 5, 30)
y = np.random.choice([1,2,3], 30, p=[0.1,0.2,0.7])
z = np.random.choice([1,2,3,4], 30, p=[0.4,0.3,0.2,0.1])
w = np.random.normal(4, 0.1, 30)
df = pd.DataFrame(np.array([x,y,z,w]).T, columns=["x", "y", "z", "w"])
g = scatterplot_matrix(df)
plt.show(g)

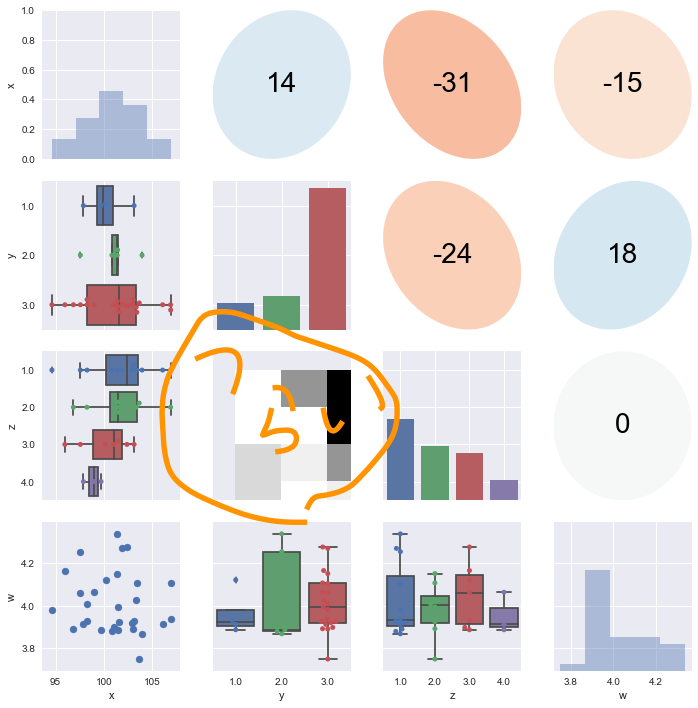
練習問題(1)

まぁほとんど弄る部分もありません。 いつも通りPyStanを回すだけです。

import pystan
import pandas as pd
import os
import pickle
from IPython.core.display import display

stan_file = os.path.join("RStanBook", "chap05", "model", "model5-3.stan")
model = pystan.StanModel(stan_file)
    
df = pd.read_csv("./RStanBook/chap05/input/data-attendance-1.txt")
N = len(df)
A = df["A"].values
Score = df["Score"].values / 200
Y = df["Y"].values
stan_data = {
    "N": N,
    "A": A,
    "Score": Score,
    "Y": Y 
}
fit = model.sampling(
    data=stan_data,
    iter=2100,
    chains=4,
    warmup=100,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

mu = fit.extract()["mu"]
diff = np.apply_along_axis(lambda x: Y - x, axis=1, arr=mu)

モデルはgithubで公開されているものをそのまま使いました。

github.com

練習問題(2)

Stanの内部の生成量を出すところで残差を計算します。 個人的には汚い部分を全部Stanの中に隠せるのでこっちのほうが好きです。

import pystan
import pandas as pd
import os
import pickle
from IPython.core.display import display

stan_file = os.path.join("RStanBook", "chap05", "model", "model5-3_kai.stan")
stan_file_c = os.path.join("RStanBook", "chap05", "model", "model5-3_kai.pkl")

# コンパイルチェック
if os.path.exists(stan_file_c) == False:
    # コンパイル済みのバイナリが無かったらstanファイルからコンパイル
    model = pystan.StanModel(stan_file)    
    with open(stan_file_c, "wb") as f:
        pickle.dump(model, f)
else:
    # バイナリがあったらそれを利用
    with open(stan_file_c, "rb") as f:
        model = pickle.load(f)
    
df = pd.read_csv("./RStanBook/chap05/input/data-attendance-1.txt")
N = len(df)
A = df["A"].values
Score = df["Score"].values / 200
Y = df["Y"].values
stan_data = {
    "N": N,
    "A": A,
    "Score": Score,
    "Y": Y 
}
fit = model.sampling(
    data=stan_data,
    iter=2100,
    chains=4,
    warmup=100,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

モデルは次の通りです。

data {
  int N;
  int<lower=0, upper=1> A[N];
  real<lower=0, upper=1> Score[N];
  real<lower=0, upper=1> Y[N];
}

parameters {
  real b1;
  real b2;
  real b3;
  real<lower=0> sigma;
}

transformed parameters {
  real mu[N];
  for (n in 1:N)
    mu[n] = b1 + b2*A[n] + b3*Score[n];
}

model {
  for (n in 1:N)
    Y[n] ~ normal(mu[n], sigma);
}

generated quantities {
  real y_pred[N];
  real diff[N] ;
  for (n in 1:N){
    y_pred[n] = normal_rng(mu[n], sigma) ;
    diff[n] = Y[n] - mu[n] ;
  }
}

つづいてpythonでグラフを描いて、目視で比較をします。

まず実測値とモデルによる予測値を比較してみます。 テキストでは予測分布を使っていますが、試しにMCMCで推定されたパラメータ分布の中央値を使って値を予測してみます。この目的は、後述する事後予測分布との比較です。これは「はじめての統計データ分析」で言うところの、条件付き予測分布を使った手法です。こちらの手法だとStanファイル中で予測をしなくていい代わりに、エラーバーをつけるのがめんどくさいです。何故ならYを導出するためのにもにも分布があるので、その両方を考慮する必要があります。今回はパスさせて下さい。

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# Aの値でindexを分類する
A0_samples = df[df["A"] == 0].index
A1_samples = df[df["A"] == 1].index

# summaryのtableからmuの中央値とsigmaを取得する
summary_df_A0 = summary_df.loc[["mu[{0}]".format(i) for i in A0_samples], :]
summary_df_A1 = summary_df.loc[["mu[{0}]".format(i) for i in A1_samples], :]
map_A0 = summary_df_A0["50%"]
map_A1 = summary_df_A1["50%"]
sigma = summary_df.loc["sigma", "50%"]

# パラメータを使って条件付き予測分布を推定する
Y_A0 = Y[A0_samples]
Y_A1 = Y[A1_samples]
Y_A0A1 = np.hstack([Y_A0, Y_A1])
Y_ast_A0 = np.random.normal(map_A0, sigma)
Y_ast_A1 = np.random.normal(map_A1, sigma)
Y_ast_A0A1 = np.hstack([Y_ast_A0, Y_ast_A1])
# グラフのために相関係数を導出する
r = np.corrcoef(Y_A0A1, Y_ast_A0A1)[0][1]

# 可視化
fig, ax = plt.subplots()
ax.plot(Y_ast_A0, Y_A0, "o", label="A=0")
ax.plot(Y_ast_A1, Y_A1, "^", label="A=1")
ax.plot([0, 0.5], [0, 0.5], "k-")
ax.legend()

# 体裁を整える
ax.set_aspect('equal')
ax.set_xlabel("Predicted value(by EAP)")
ax.set_ylabel("Observed value")
ax.set_title("r={0}".format(r))
plt.show()

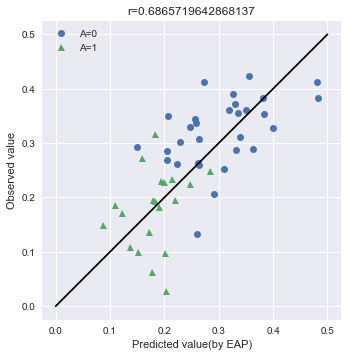
Aについてバラけているわけではないですが、あまり精度が良く無さそうです。モデルの精度が良くないのでしょうか(後述しますが、これは違います)?

続いて、MCMCサンプリングの中でyの予測値を推定します。これは「はじめての統計データ分析」で言うところの、事後予測分布を使った手法です。こちらのほうが分布全体を考慮して行っているので、正確な予測値を計算することが出来ます。エラーバーについてもMCMCの分布を使えばいいので簡単です。今回は教科書の80%区間ではなく、デフォルトで計算される75%区間を利用しています。

# Aの値でindexを分類する
A0_samples = df[df["A"] == 0].index
A1_samples = df[df["A"] == 1].index

Y_A0 = Y[A0_samples]
Y_A1 = Y[A1_samples]
Y_A0A1 = np.hstack([Y_A0, Y_A1])

# プロット点の計算
summary_df_A0 = summary_df.loc[["y_pred[{0}]".format(i) for i in A0_samples], :]
summary_df_A1 = summary_df.loc[["y_pred[{0}]".format(i) for i in A1_samples], :]
Y_pred_A0 = summary_df_A0["50%"]
Y_pred_A1 = summary_df_A1["50%"]
Y_pred = np.hstack([Y_pred_A0, Y_pred_A1])
# 誤差の計算
Y_pred_A0_err_down = (Y_pred_A0 - Y_pred_summary_A0["25%"]).values
Y_pred_A1_err_down = (Y_pred_A1 - Y_pred_summary_A1["25%"]).values
Y_pred_A0_err_up = (Y_pred_summary_A0["75%"] - Y_pred_A0).values
Y_pred_A1_err_up = (Y_pred_summary_A1["75%"] - Y_pred_A1).values
Y_pred_A0_err = np.vstack([Y_pred_A0_err_down, Y_pred_A0_err_up])
Y_pred_A1_err = np.vstack([Y_pred_A1_err_down, Y_pred_A1_err_up])
# 相関係数の計算
r = np.corrcoef(Y_A0A1, Y_pred)[0][1]

# 可視化
fig, ax = plt.subplots()
ax.errorbar(Y_pred_A0, Y_A0, yerr=Y_pred_A0_err, fmt="o", label="A=0")
ax.errorbar(Y_pred_A1, Y_A1, yerr=Y_pred_A1_err, fmt="^", label="A=1")
# y=xの線を書く
ax.plot([0, 0.5], [0, 0.5], "k-")
# 凡例をつける
ax.legend()

# 体裁を整える
ax.set_aspect('equal')
ax.set_xlabel("Predicted value")
ax.set_ylabel("Observed value")
ax.set_title("r={0}".format(r))
plt.show()

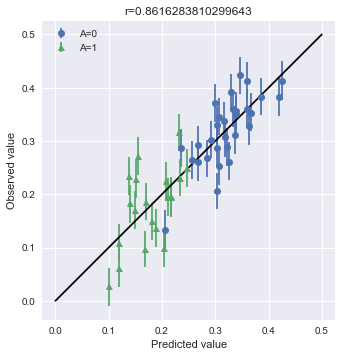
結果がわりと異なります。相関係数に如実に現れました。条件付き予測分布ではダメかと思ったモデルですが、こちらでは問題がなさげなことが推定されます。以上のことから、条件付き予測分布はオンラインで利用できるなどの利点がありますが、その分結果の浮動性があることを頭に入れたほうが良いと思います。とはいえ、どちらの方法でもAに関する偏ったバラつきが無いことはわかりますので、何を見たいかの使い分けが結局のところ肝心です。

最後に実測値とパラメータの誤差を調べます。

summary_df_diff = summary_df.loc[["diff[{0}]".format(i) for i in range(0, 50)], :]

fig, ax = plt.subplots()
sns.distplot(summary_df_diff["50%"], bins=np.arange(-0.15, 0.15, 0.03), ax=ax)
ax.set_xlabel("Epsilon EAP")
ax.set_ylabel("Count")
plt.show()

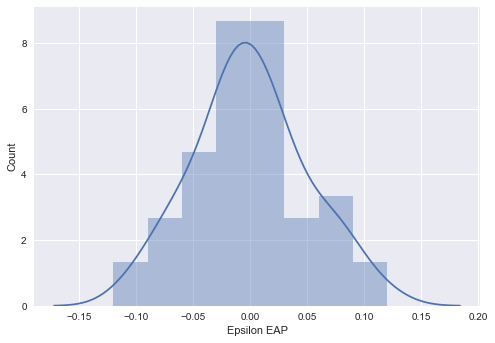
教科書の結果から分かっていましたが、きちんとあてはめた正規分布に従っています。

練習問題(3)

離散値と離散値の集計です。pandasのpivot_tableメソッドを使えばいいのですが、芸がないのでヒートマップで可視化しておきます。AとYの各組み合わせで足していけばいいので、ラムダ式を読み出してlenでカウントしました。

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

df = pd.read_csv("./RStanBook/chap05/input/data-attendance-3.txt")
pdf = df[["A", "Y"]].pivot_table(index="A", columns="Y", aggfunc=lambda x:len(x))
g = sns.heatmap(pdf, annot=True)
plt.show(g)

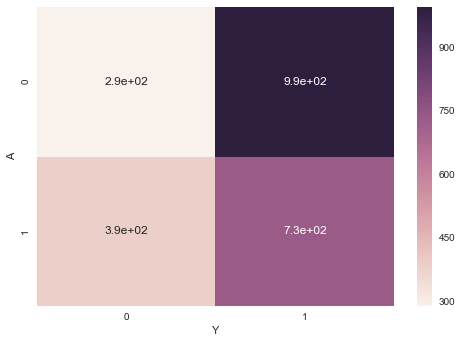
練習問題(4)

晴れがもたらす影響を基準値として、曇と雨が持つ影響についてもMCMCから推定してみます。これだけだと芸が無いので、WAICによるモデルのフィッティングについても評価してみます。

import pystan
import pandas as pd
import os
import pickle
import numpy as np
from IPython.core.display import display
from logging import getLogger, Formatter, StreamHandler, DEBUG

# printではなくloggerを使う
def get_logger():
    logger = getLogger(__name__)
    logger.setLevel(DEBUG)
    log_fmt = '%(asctime)s : %(name)s : %(levelname)s : %(message)s'
    formatter = Formatter(log_fmt)
    stream_handler = StreamHandler()
    stream_handler.setLevel(DEBUG)
    stream_handler.setFormatter(formatter)
    logger.addHandler(stream_handler)
    return logger
logger = get_logger()

stan_file = os.path.join("RStanBook", "chap05", "model", "model5-5_kai.stan")
model = pystan.StanModel(stan_file)    
    
trans = {"A": 1, "B": 2, "C": 3}
df = pd.read_csv("./RStanBook/chap05/input/data-attendance-3.txt")
I = len(df)
A = df["A"].values
Score = df["Score"].values / 200
W = df["Weather"].values
W = np.array([trans[w] for w in W])
Y = df["Y"].values
stan_data = {
    "I": I,
    "A": A,
    "Score": Score,
    "W": W,
    "Y": Y 
}
fit = model.sampling(
    data=stan_data,
    iter=1200,
    chains=4,
    warmup=200,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

log_lik = fit.extract("log_lik")["log_lik"]
waic = -2 * np.sum(np.log(np.mean(np.exp(log_lik), axis=0))) + 2 * np.sum(np.var(log_lik, axis=0))
logger.info("WAICの値は{0}です".format(waic))

モデルは以下の通りです。

data {
    int I;
    int<lower=0, upper=1> A[I];
    real<lower=0, upper=1> Score[I];
    int<lower=1, upper=3> W[I];
    int<lower=0, upper=1> Y[I];
}

parameters {
    real b[3];
    real b_w[2] ;
}

transformed parameters {
    real q[I];
    real beta_w[3] ;
    beta_w[1] = 0 ;
    beta_w[2] = b_w[1] ;
    beta_w[3] = b_w[2] ;

    for (i in 1:I)
        q[i] = inv_logit(b[1] + b[2]*A[i] + b[3]*Score[i] + beta_w[W[i]]);
}

model {
    for (i in 1:I)
        Y[i] ~ bernoulli(q[i]);
}

generated quantities {
    real log_lik[I] ;

    for (i in 1:I){
        log_lik[i] = bernoulli_lpmf(Y[i]|q[i]) ;
    }
}

さて経験的にパラメータを決定した時と比べて、WAICはどうなったでしょうか。

• 経験的に決めた場合 : WAIC=2769
• MCMCからサンプリングした場合: WAIC=2764

ちょっとだけ、MCMCからサンプリングした場合のほうが値が良くなります。EAPを見てモデルを書いてみると

• 経験的に決めた場合

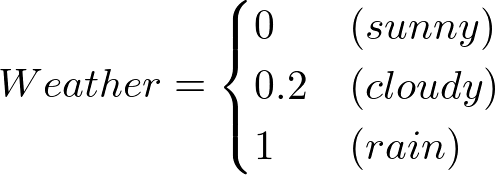
• MCMCからサンプリングした場合

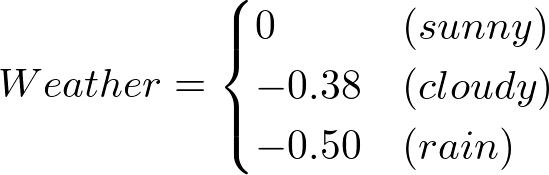
となります。Weatherの部分も係数の-0.45を考慮すると、そこまで変わりません。僕は経験的に得られた0:0.2:1が結構いいものであったと解釈しました。

つづいてpythonでグラフを描いて、目視で結果を比較します。 テキストに描いてあるように、ロジスティック回帰の観測値は0/1になるので、可視化が難しいところです。qの値が、データからどのように変化するかを調べます。テキストの例では連続値のScoreと離散値のAが可視化されています。

まずScoreの影響を可視化します。

• 推測したqの中央値をデータと対応付けるために、indexを振り直します。
• カラムを複数使ったデータの選択なので、queryメソッドで取得します。
• qの中央値の線をきれいに書くためにソートを挟んでいます

# qの値を取得
summary_df_q = summary_df.loc[["q[{0}]".format(i) for i in range(0, I)], :]
q_range = summary_df_q[["25%", "50%", "75%"]]
q_range.index = range(len(q_eap))
# データと結合(順番はこの時点では保存されている)
df_concat = pd.concat([df, q_range], axis=1)
# 一部のデータだけ選択
df_filtered = df_concat.query("A == 0 & Weather == 'A'")
df_filtered = df_filtered.sort_values("Score")

# Yの点の位置をそれぞれちょっとずらす
y_randomized = [y + np.random.normal(0, 0.05) for y in df_filtered["Y"]]

# 可視化
fig, ax = plt.subplots()
ax.plot(df_concat_filtered["Score"], df_concat_filtered["50%"], "k-")
ax.fill_between(df_concat_filtered["Score"], df_concat_filtered["25%"], df_concat_filtered["75%"], facecolor="pink")
ax.plot(df_concat_filtered["Score"], y_randomized, "o", label="Y")
ax.legend()
ax.set_xlabel("Score")
ax.set_ylabel("q")
plt.show()

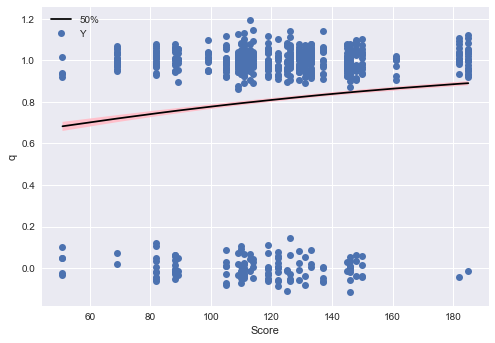
次にAに対するプロットを書きましょう。matplotlibで頑張るのが面倒だったのでseabornで書きました(なんかごめんなさい)。適材適所です！

# qの値を取得
summary_df_q = summary_df.loc[["q[{0}]".format(i) for i in range(0, I)], :]
q_range = summary_df_q[["25%", "50%", "75%"]]
q_range.index = range(len(q_eap))
# データと結合(順番はこの時点では保存されている)
df_concat = pd.concat([df, q_range], axis=1)

# 可視化
fig, ax = plt.subplots()
sns.violinplot(data=df_concat, x="50%", y="Y", ax=ax, orient="h")
sns.swarmplot(data=df_concat, x="50%", y="Y", hue="A", ax=ax, orient="h", palette=sns.color_palette("Set2", n_colors=2))
ax.set_xlabel("q")
ax.set_ylabel("Y")
plt.show()

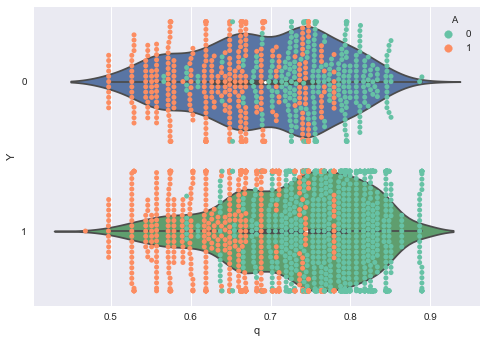
最後にROCカーブを書いて、AUCを計算します。これについてはScikit-learnを使うのが簡単でしょう。

from sklearn.metrics import roc_curve, roc_auc_score

summary_df_q = summary_df.loc[["q[{0}]".format(i) for i in range(0, I)], :]
q = summary_df_q["50%"]

# AUCの計算
auc = roc_auc_score(Y, q)

# ROCカーブの座標を計算
false_positive_rate, true_positive_rate, _ = roc_curve(Y, q)
fig, ax = plt.subplots()
ax.plot(false_positive_rate, true_positive_rate)
# y=xを描く
ax.plot([0, 1], [0, 1], "k-")

# 体裁を整える
ax.set_aspect('equal')
ax.set_xlabel("False Positive Rate")
ax.set_ylabel("True Positive Rate")
ax.set_title("AUC = {0}".format(auc))
plt.show()

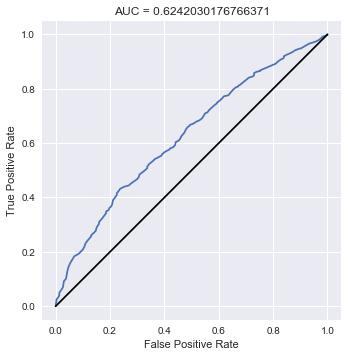
練習問題(5)

import matplotlib.pyplot as plt
import os
import pandas as pd
import pickle
import pystan
from IPython.core.display import display

stan_file = os.path.join("RStanBook", "chap05", "model", "model5-6b.stan")
model = pystan.StanModel(stan_file)    
    
trans = {"A": 1, "B": 2, "C": 3}
df = pd.read_csv("./RStanBook/chap05/input/data-attendance-2.txt")
N = len(df)
A = df["A"].values
Score = df["Score"].values / 200
M = df["M"].values
stan_data = {
    "N": N,
    "A": A,
    "Score": Score,
    "M": M 
}
fit = model.sampling(
    data=stan_data,
    iter=2100,
    chains=4,
    warmup=100,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

Mpred = np.median(fit.extract()["m_pred"], axis=0)
fig = plt.figure(figsize=(5,5))
ax = fig.gca()
ax.plot(Mpred, M, "o")
ax.plot(range(0, 100), range(0, 100))
ax.set_xlim(0, 100)
ax.set_ylim(0, 100)
ax.set_xlabel("Predicted")
ax.set_ylabel("Measured")

plt.show(ax)

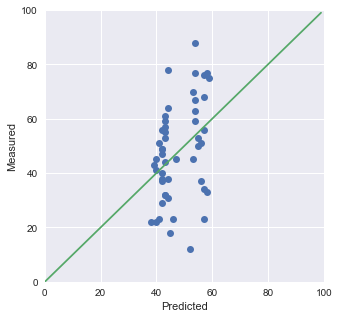
全然y=xに乗っていません…(合っているのかめちゃめちゃ不安です)。

この結果からは、予測が出来ていないことが分かります。説明変数が足りてないということですね。よくあることですが、計測が終わった後にこうなった場合は、新しくメタデータを足して計測し直しになるわけです。つらい。

練習問題(6)

練習問題(5)と(6)はちょっと気をつける必要があります。アヒル本だけ読んだ時には「処理」の違いというものが

• 両方に別々の処理を施した
• 片方には処理を施して、片方には何もしなかった

という2つのパターンのどちらなのか分かりません。前者の場合にはベースラインとなるものに別々の効果が生じることを予測できますが、後者の場合には一方だけはベースラインのままで、もう一方に何か効果が現れることになります。

データの元となった緑本を読んでみると、後者であることが分かります。前者を踏まえてモデルを作ってみると、MCMCが収束せずに頭を悩まるハメになります(僕は緑本を読んだはずなのに忘れていて喘ぎました)。

前者の場合でも相対的な効果を踏まえると同じじゃないの？と思っていたのですが収束しないですし、そうではないんですね。ちょっとした発見でした。これはChapter 10の一番初めに出てくる識別可能性の問題に引っかかるからですね。

import pystan
import pandas as pd
import os
import pickle
from IPython.core.display import display

stan_file = os.path.join("RStanBook", "chap05", "model", "practice6.stan")
model = pystan.StanModel(stan_file)    
    
trans = {"C": 0, "T": 1}
df = pd.read_csv("./RStanBook/chap05/input/data3a.csv")
N = len(df)
X = df["x"].values
F = df["f"].values
F = np.array([trans[x] for x in F])
Y = df["y"].values
stan_data = {
    "N": N,
    "X": X,
    "F": F,
    "Y": Y 
}
fit = model.sampling(
    data=stan_data,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

モデルは次です。

data {
    int N;
    real<lower=0> X[N];
    int<lower=0, upper=1> F[N];
    int<lower=0> Y[N];
}

parameters {
    real b[3] ;
}

transformed parameters {
    real<lower=0> lambda[N] ;

    for (n in 1:N){
        lambda[n] = exp(b[1] + b[2]*X[n] + b[3] * F[n]) ;
    }
}

model {
    for (n in 1:N){
        Y[n] ~ poisson(lambda[n]);
    }
}

練習問題(7)

(6)と同様に処理の効果にだけ気をつけて下さい。

import pystan
import pandas as pd
import os
import pickle
from IPython.core.display import display

stan_file = os.path.join("RStanBook", "chap05", "model", "practice7.stan")
model = pystan.StanModel(stan_file)    
    
trans = {"C": 0, "T": 1}
df = pd.read_csv("./RStanBook/chap05/input/data4a.csv")
I = len(df)
N = df["N"].values
X = df["x"].values
F = df["f"].values
F = np.array([trans[x] for x in F])
Y = df["y"].values
stan_data = {
    "I": I,
    "N": N,
    "X": X,
    "F": F,
    "Y": Y 
}
fit = model.sampling(
    data=stan_data,
    iter=1500,
    chains=4,
    warmup=500,
    seed=1234,
)
summary = fit.summary()
summary_df = pd.DataFrame(
    summary["summary"],
    index =summary["summary_rownames"],
    columns=summary["summary_colnames"]
)
display(summary_df)

モデルは以下の通りです。

data {
    int I;
    int<lower=0> N[I];
    real<lower=0> X[I];
    int<lower=0, upper=1> F[I];
    int<lower=0> Y[I];
}

parameters {
    real b[3] ;
}

transformed parameters {
    real<lower=0> q[I] ;

    for (i in 1:I){
        q[i] = inv_logit(b[1] + b[2]*X[i] + b[3]*F[i]) ;
    }
}

model {
    for (i in 1:I){
        Y[i] ~ binomial(N[i], q[i]) ;
    }
}

練習問題(4), (6)と(7)は初めに取り組んだ時に、モデルが全然収束しなくて足踏みしました。そういう時にはMCMCサンプリングが無理をして変な部分を探索しようとするのでめちゃめちゃ時間がかかります。なので待機時間で「失敗したな」と悟れたりするのはちょっと面白いところです。