Easy to type

個人的な勉強の記録です。データ分析、可視化などをメイントピックとしています。

StanのMAP推定の収束判定についてのコードを読む

ベイジアンモデリング

概要

Stanではoptimizing関数(R)/メソッド(Python)を使うことで尤度関数の最大化を実施することができます。デフォルトではL-BFGSアルゴリズムが使われているのですが、これに対する収束は幾つかのパラメータで制御されています。そのメモ記事です。

もし収束判定についてよく分かっていない場合、勾配を使った数値計算における収束判定については、ネットの記事だと九大の渡部先生が書いたものなんかが良いかと思います。

収束判定のパラメータ

PystanのAPIページによると、次の5つが挙げられています。StanはC++で書かれたコアライブラリを各言語のラッパーから呼び出す形式になっているので、特にRStanやJuliaStanでも、この部分に差はありません。

  • tol_obj (float, optional) – For BFGS and LBFGS, default is 1e-12.
  • tol_rel_obj (int, optional) – For BFGS and LBFGS, default is 1e4.
  • tol_grad (float, optional) – For BFGS and LBFGS, default is 1e-8.
  • tol_rel_grad (float, optional) – For BFGS and LBFGS, default is 1e7.
  • tol_param (float, optional) – For BFGS and LBFGS, default is 1e-8.

Stanのコード

これらのパラメータがStanのコード中で使われているのは、次の部分となります。

ここでif文の判定に使われているPropertyが設定されているのは、次の部分になります。

ここで出されたシグナルの結果を受けて、次のコードで標準出力に収束判定についてのメッセージが出力されます。

コードより分かること

このコードを読んでみると、利用するパラメータのうち、tol_rel_objとtol_rel_gradが何故かやたら大きな値である理由が分かります。それぞれの値について、計算機イプシロンが掛けられているのです。自分のmacOSの環境ですと、C++のScalar(これはdouble型であるとコード中で定義されています)の計算機イプシロンは2.22045e-16と表示されました。なので、例えばtol_rel_gradの例になりますと、API側で入れる値は1e+7なのですが、実際の判定では2.22045E-13より小さかった場合に収束、と判定されていることが分かります。

DockerでPyomo+Jupyterlabの実行環境をパッケージ化

最適化モデリング

概要

ajhjhaf.hatenablog.com

このブログの技術関連で最もアクセスとかコメントを頂けるのはこの記事です。その関係もあってか、インストール方法についての質問がたまに飛んできました。

自身でも同じ計算環境をもう一度作るのがかなりしんどそうだな、と思ったので、Dockerを使った再現環境を作成してみました。上述しているソルバーの内、ライセンス的に商用では使えないCPLEX以外*1が使えます。pyomoでMINLPを試してみたい場合はこれで大丈夫ではないでしょうか。

使い方

リポジトリはこちらです。

github.com

詳細はREADMEに書いてあるとおりです。SCIPはライセンス的には再配布可能ですが、それもアカデミック利用に限られる…とややこしいのでリポジトリには入れていません。別途ダウンロードする必要があります。 ダウンロード後、SCIPやコンテナ内でいじっているソルバーのバージョンがREADMEに有るものと同一ならば

docker-compose up -d --build

でビルドが始まり、コンテナが立ち上がります。ソルバーのビルドにはかなり時間がかかりますのでご注意ください。完成したイメージファイルは当環境で778MBとなりました。

皆様の最適化計算の一助と成れば幸いです。

*1:SCIPも本来使えませんが、コメントで質問されたのがSCIPだったので組み込んであります。外部ファイルに依存してしまうのでdockerhubには登録出来なくなりましたが

こうしてGoogleに落ちた

自己紹介

TL;DR Leetcodeをもっとやる必要がありました

Googleの社員が選考過程についてブログを書いています。ちょっと前にNTTブームを引き起こしたid:kumagiさんとか。

kumagi.hatenablog.com

ところで、僕もGoogleの選考をわずか一ヶ月前に受け、そして落ちました。いずれ記事にしてみたいなとは思っていたのですが、社内の方々が記事にしているのを見て秘密保持のレベルが判断できたので、ブームの内に自分でもまとめてみます。

人物

リクルーターと接触する前の状態です。

特徴量

  • 非情報[科学|工学]専攻の工学系
  • 国立大
  • D2
  • M1からは情報系のリーディング大学院に所属(情報系のフォーマルなクラスはそこでいくつか取得した程度)
  • B4からデータ解析の研究室に所属
  • D1時に非英語圏へ3ヶ月の研究留学
  • DC1持ち
  • Computer ScienceのPublication無し
  • 5段階でレベルをつけると、

といった感じです。見れば分かる通り、情報系のまともな教育を受けていません。早いシステム言語も大して書けません。

英語

博士学生ですし、自身の分野も情報系と同じく海外の方が圧倒的に進んでいるので、英語論文は読んでましたし、書いてました。ただTOEIC自体は6年前に取った650程度のスコアがあるだけです。その点数を実際に先方へ報告しました。ただ後述するように選考の過程で英語力を評価されるタイミングはありましたが、社員の方から「英語力大丈夫？」みたいなあまり意味のない質問をされたことはありませんでした。実力本位ですね。

これはGoogleにも限られないので課程を終えられたら書くつもりですが、就活全体を通して自身の英語力は前述した研究留学の経験が一つのバロメータとして評価されていたように思えます。最近はトビタテ！とか、学振持ちなら海外渡航支援などもありますので、是非とも実力証明として留学をしましょう。そして面白い研究をしましょう。

競技プログラミング

まったく経験がありません。……この時点でSoftware Engineerに応募したことが間違っている気もします。ブログの過去記事の通り、僕はデータ分析側に興味があり、基礎アルゴリズムとデータ構造の勉強は疎かにしてしまいました。研究もアルゴリズムを考えるより、既存の手法で問題を解く方がメインです。

リクルーターとの接触

アカリクの逆採用型ITイベントで接触しました。このイベント自体も、自身で能動的に参加したわけではなくアカリク側から連絡があって受動的に参加したのですが、自分が思っていたよりいろいろな会社と話せて楽しかったです。そもそも自分自身がああいう初対面の人にPRをガンガンかけていく場が得意ということも一つの発見でした。おすすめです。

イベントの接触時には、人事社員1+現場社員1でした。イベントに応募した時点で、自分のポートフォリオスライドを作ってくるようにアカリクから指示が出されたので、それを使って自己紹介、先方からの質問といった形式です。1つ嬉しかったのは、Googleがそもそも僕のブースに来てくれた理由として学振持ちということを見てくれたことです。この点に着目してくれたのはミクシィとGoogleだけでした*1。努力した点を評価してくれるのは、何にとっても嬉しいものです。

現場社員の方は自身のエンジニア的な活動の取り組みに技術的な質問を投げかけてきて、人事の方はこちらからの非技術的な質問に答えるのがメインの役割だった気がします。もちろん、Googleという会社像についての非技術的な質問もあり、僕がよく考えずに回答したことに対してダメ出ししてきたのが面白かったです。

面談の最後には、コーディング面接を模擬的にやってくれました。この問題自体は簡単でしたが、自分がビッグオー記法を完全に理解していなかったり、計算効率が悪い回答を答えたりした凡ミスがありました。

イベント後、研究室に戻ってお礼メールを各社に送信。イベント自体は土曜日でしたが、月曜日になってから、一番最初にメールが帰ってきたのがGoogleでした*2。CV提出と引き換えに選考を進めてもらえるとのことでしたが、当時論文を提出するために格闘していたため、正式な応募まで時間的猶予をもらいました。

この段階でGoogleの選考プロセスをまともに調べて、コーディング面接の対策が必要だったという点もpendingにした一因です。イベントの間に仲良くなった別の参加者から、Googleの面接ではHacking the Coding Interview(HtCI)という本が良いらしい！和訳版もある。と教えてもらって読んだり、TwitterやGoogleで「Google 採用」と調べたアドバイスに従ってLeetcodeで遊んだりしてました。

世界で闘うプログラミング力を鍛える本 ~コーディング面接189問とその解法~

世界で闘うプログラミング力を鍛える本 ~コーディング面接189問とその解法~

leetcode.com

落ちた身なので全く説得力のないアドバイスですが、Leetcodeをやる場合にはExplore -> Top Interview Question、へ取り組むのが良いと思っています。Easy, Medium, Hardに分かれているので、慣れているならHardとかやって一通りさらったあとに個別の問題へ移ればいいですし、僕の場合みたいに時間も経験もないならEasyからMediumへと進めていけます。ちなみにいま確認したらSolvedが60でした。確かに体感的に足りてないですし、400問ぐらい解いておくと良いらしいです。

ただ僕のように付け焼き刃でやっても仕方がないことですし、HtCIにも書いてあるとおり普段からLeetcodeなりやって自力を付けておくのがベストです。走り込みみたいなもんです。皆様が僕の屍を乗り越えて、LeetcodeへSign inしてくれることを期待しています。

電話面接

電話面接は2回ある場合が報告されていますが、僕の場合は1回でした。アカリクイベントの会話で1回分の面談が免除されたのかもしれません。Google docsで問題を解く形式です。いろいろな人が報告していたり、HtCIに書いてあるようにも問題自体は難しくありませんでした。全然華麗に解けなかったけど。それでも45分で解いて、電話面談は無事にパスしました。

電話面談をパスしたあともLeetcodeでの勉強は続けたり、先方から言われた面談予告の内容に対応した勉強をしていました。Web系の基礎固めをしたいと考えて

Webを支える技術 -HTTP、URI、HTML、そしてREST (WEB+DB PRESS plus)

Webを支える技術 -HTTP、URI、HTML、そしてREST (WEB+DB PRESS plus)

を読んだり、Software Engineerでも人材募集ページに書かれているような思考力の問題が出されるかもしれないと考えて

FACTFULNESS(ファクトフルネス)　10の思い込みを乗り越え、データを基に世界を正しく見る習慣

FACTFULNESS(ファクトフルネス)　10の思い込みを乗り越え、データを基に世界を正しく見る習慣

を読んだり、一般論を知りたいと考えて

CAREER SKILLS　ソフトウェア開発者の完全キャリアガイド

CAREER SKILLS　ソフトウェア開発者の完全キャリアガイド

を読んだりしました。このうちWebを支える技術は、基礎技術の組み合わせでWebができている点を認識できて面白かったのでオススメです。Webの記事だと

qiita.com

なんかもいいと思います。

オンサイト面接

面接は5回でした。メールでは4回と聞いていたので5回目があると分かった時には、やりきった感(やりきってない)に満たされた+疲れ、でしんどかったです。オンサイト面接の形式は他の方のそれとほとんど同じです。なので割愛。英語3回、日本語2回でした。今思い返せば、この時点で僕の英語力を先方が非常に疑問視していることが推測できます。

問題はそこそこ解けた気もしていますが、きっと思い出補正で、落ちたからにはボーダーラインに達していないぐらいには全然出来ていなかったのでしょう。

1つの大きな原因として、時間を気にして練習問題を解いていなかったことが挙げられます。問題を見て分からなかった瞬間に答えを見るのは意味がありませんが、長々と考える癖を付けてしまうのも良くなかったわけです。時間制限のあるコンテスト型の競技プログラミングサイトで練習するとか、LeetcodeやHtCIの問題を解くにしても制限時間を付けてプレイするほうが良いでしょう。例えば面接が1つ30分と考えたら、5分問題把握、10分でアイディアリング、10分で実装、5分でテストといった流れが考えられます。だとしたら、練習の場合でも同じ時間配分で解いたほうが良くないですか？分からなかったら先程の400問の例のようにパターンを網羅するため、答えをみてアイディアを理解してから、コードを移さずに自分で実装してみるのが良いかと思います。

面接外の1つの大きなポイントは、なんといってもGoogleの社内に入れるということです。様々な驚きポイントがありました。

  • (当たり前だけど)ゲストを社内で1人にしてはいけないらしい。常に社員の方がそばにいて、気を使わせているようで申し訳なかった。
  • 伝説ともなっている昼食のバイキングは超豪華だった。具体的には、自分が行った日はむき身のカニが食べ放題だった。
  • 本当に自販機にお金を入れるところがなかった。
  • etc...

で、1週間後に落選通知が来ました。残念だった点として、Googleが出しているreWorkでは落選者にはフィードバックをしよう、と書かれていますが、僕にはその点は何も通知されませんでした。逆にアンケート調査もありませんでした。なかなか自分のエンジニアリングについて評価して貰える(しかもGoogleの社員に！)機会は無いので僕も期待していたのですが、全員に対して適用されるものではないようです。

敗因

上述した理由の

  • 情報工学の基礎的な教養が不足していた
    • 特にデータ構造は本当に弱いことがわかった。データサイズが大きくないので、Treeとか使わないで済んでしまう
  • 英語力とコミュニケーションの不足
  • 実際の形式と練習の形式の不一致

は特に大きな理由と考えられますが、マインド面からくる手抜きの影響も否定できません。僕も受かると思っていなかったので、「有名な社食を食べに行くか～～」と思って対策をしていた節があります。「なんとしても採用されて、面白いプロダクトを作るぞ！！」といった強い気持ちは本番のパフォーマンスというより、日々の努力のために役に立ちます。そういうハングリーさは完全に欠けていました。

まとめ

ソフトウェアエンジニアなので間違いなくアルゴリズムとデータ構造を理解しておく必要があります。Leetcodeで対策しましょう。

ちなみに僕が選考を受けてみようと思ったのは今年は選考に受かりやすいと予想したからです(それは間違いだったわけですが)。Googleは来年度には渋谷ストリームへオフィス移転します。

toyokeizai.net

14～35階のオフィスフロア22階分を借り切り、現在の従業員（1300人）の2倍を収容できるという。

これを読んで、空いたスペース分社員を補充するために入りやすいんじゃないか？と考えたわけです。しかしGoogleはハードルの高さに妥協しないことで有名でしたし、そのとおりだったわけです。そういう憧れの会社であり続けてくれる点は、個人的にはちょっと嬉しいです。

*1:余談ですが、ミクシィもこの後採用プロセスに進みました。自分が就活した中で最も素晴らしい選考体験だったので、おすすめです。

*2:全体を通してGoogleはメールの返信が早くてよかった

ScipyでBrunner-Munzel検定

解析

概要

Brunner-Munzel検定は、不当分散のときに使えるノンパラメトリック検定です。ランクから、得られたデータの中央値に有意差があるか検出します。 ノンパラメトリックの検定では、Wilcoxon-Mann-WhitneyのU検定が非常に有名ですが、この検定は不当分散の場合には第一種の過誤を得る確率が5%にならない場合があり、適切な手法として使えません。 詳しい調査には、以下のような先行記事があります。

hoxo-m.hatenablog.com

Brunner-Munzel検定

二群の平均値（代表値）の差を検定するとき

しかしBrunner-Munzel検定は、有用性のわりにどマイナーな検定なので、Rではlawstatというパッケージで利用が出来ましたが、Pythonにはパブリックで使えるいい感じのライブラリがありませんでした。 今回アップデートされたScipy Version 1.2.0でBrunner Munzel検定が使えるようになりました。使い方の記録です。

使い方

ドキュメントはこちらです。上述した奥村先生の記事と全く同じやり方にしてみます。

from scipy.stats import brunnermunzel

a = [1,2,1,1,1,1,1,1,1,1,2,4,1,1]
b = [3,3,4,3,1,2,3,1,1,5,4]
brunnermunzel(a, b)

結果

BrunnerMunzelResult(statistic=3.1374674823029505, pvalue=0.005786208666151538)

統計値やP-valueも一致しました。デフォルトでは、統計値をt分布に当てはめて推定しています。 原著論文中ではサンプルサイズが50未満であるときにはこちらを利用し、それ以上だと正規分布に対して当てはめています。正規分布に対して使いたい場合はdistributionのオプションをnormalに変更すれば使えます。 検定を両側、片側でやる場合にはalternativeが使えます。

皆様も、ぜひBM検定を使って「まだ不等分散で消耗してんの？？」とドヤ顔してください。

本文

さて、この記事の目的はBM検定の宣伝でもあるのですが、真の目的はScipyにCommitする感想です。このBM検定、及びScipyのAPIドキュメント*1は僕が書きました。当該PRはこちらです。 自身のメイン言語がPythonだったこともあり、BM検定は有用そうでしたから、車輪の再開発で消耗するような人を減らしてみたかったという想いで取り組みました。 僕はOSSにコミットするのは、ほぼ初めてだったのでとてもいい勉強になりました。以下箇条書きです。

  • コード規約について
    • 基本的に、WMW検定の書き方へ似せた。ドキュメントも同じ。似た構造の検定なので、悪い戦略ではなかっただろう。
    • Scipyではgitのコミットメッセージにも規約がある。自身はそれまで非常にテキトーなコミットメッセージを書いていたので、一つの目安として自分のその他のプロジェクトでも使うようになった。
    • 自動シンタックスチェッカーを入れてFlake8で静的テストするようになった。
  • コードレビュー
    • しょーもない変数の使い方などについてもコメントをくれた。
    • 科学計算をする上で桁落ちや型変換によるエラーは大きな問題だが、それについて指摘してくれ、気がつくことが出来た。以降わりと気を使っている。
  • マージまで
    • 非常に時間がかかった。
    • 最初にコミットしたのが2017年4月だったわけだが、放置され気味でmasterにマージされるのに1年放置。
    • 何故か当初予定していたMilestone(1.1.0)から一つ先送りにされて、1.2.0でようやくマージ。結局Stagingされるまでは1年と8ヶ月かかった。
    • 1Milestoneが約半年で締められ300commit進むこと、オーガナイザーの苦労を考えると仕方ないが、もうちょっとなんとかならないのかなと思わなくはない(ガンガン貢献してオーガナイザーとして働け、というデカイまさかりが飛んできそう)。

また機会があれば、Scipyに限らずOSSに取り組んでみたいです。

*1:今読むと文法ミスが多くてしんどい。

Stanで非閉型な逆関数を含む分布のモデリング

ベイジアンモデリング

概要

この記事はStanアドベントカレンダー-5日目の記事です(冗談です)。 趣味でやっている円周分布の勉強もそこそこ進みました。この記事では、清水本に載っている逆Batchelet変換(Inverse batschelet transformation)を使った分布をStanで実装して、現時点での問題点について考察します。

角度データのモデリング (ISMシリーズ:進化する統計数理)

角度データのモデリング (ISMシリーズ:進化する統計数理)

背景

円周分布として有名なものとして、von Mises分布、心臓分布、巻き込みコーシー分布などがあります。しかしこれはいずれも平均パラメータで最頻値(=モード)を取り、その左右に集中度パラメータに応じた分散が対称に存在する分布です。しかし実際のデータでは、どちらかの方向に分散が偏ることがあります。このような非対称分布の拡張は円周分布のみならず、正規分布などでも考察されています。日本語資料でしたら豊田黄色本などに記述があります。

実践 ベイズモデリング -解析技法と認知モデル-

実践 ベイズモデリング -解析技法と認知モデル-

さて円周分布では、次のような拡張があります。

Sine-skewed distirbution

清水本の中では、非対称な円周分布を構築する方法の一つとして正弦確率摂動法によるSine-skewed分布が載せられています。原著論文は(Abe, 2011)です。

link.springer.com

この分布は確率密度関数の設計が簡単なので、推定が容易というメリットがあります。更に確率密度関数の全区間の積分値である \int_{-\pi}^{\pi}p(\theta)d\theta = 1という式が保持され、正規化が不要です。その一方で分散が集中度パラメータ(concentration parameter)だけでは制御されず、歪度パラメータからも影響を受けてしまう欠点があります。

Batschelet transformation

一方で、もともと円周分布を歪ませる方法としては(Batschelet, 1981)で提案された方法が有名です。

この方法では、 vonmises(\theta|\mu, \kappa)を基に、 aevonmises(\theta | \mu, \kappa, \nu) = vonmises(\theta + \nu\cos(\theta - \mu) | \mu, \kappa)と変換を加えます。この方法は分かりやすいし簡単なのですが、 \int_{-\pi}^{\pi}aevonmises(\theta|\mu, \kappa, \nu) d\theta = 1が維持されません。そのためvon Mises分布とは確率密度関数の形がやや変わり、 aevonmises(\theta|\mu, \kappa, \nu) = \frac{\exp(\kappa(\cos(\theta - \mu + \nu\cos(\theta - \mu)))}{c_{\mu, \kappa, \nu}}となります。 c_{\mu, \kappa, \nu}は正規化定数で、 c_{\mu, \kappa, \nu} = \int_{-\pi}^{\pi} \exp(\kappa(\cos(\theta - \mu + \nu\cos(\theta - \mu)))により求められます。確率密度関数の和が1となるように、全区間で積分して和を取り、割るという至極単純なアイディアです。

しかしこの計算は積分が入って面倒です。この記事では扱いませんが、現時点ではStanに積分機能が無いので、合成シンプソン法などの数値計算で代替するのが一つのアイディアになります。なお(Batschelet, 1981)は絶版になり手に入りませんが、(Abe, 2013)でより一般的に拡張されて説明されてますので、そちらを参考にすると良いかと思います。

link.springer.com

Inverse Batschelet transformation

(Jones&Pewsey, 2012)では、逆変換 s(\theta) = t^{-1}_{1, \nu}(\theta)をかませることで、正規化が不要な非対称分布を作りました。 t^{-1}_{1, \nu}(\theta)は t_{1, \nu}(\theta) = \theta -\mu - \nu(1 + \cos(\theta-\mu)の逆関数です。s(t)は閉型(closed-form)で、つまり簡単な形で表すことが出来ません。このような逆関数の変換を含んだ分布の例を殆ど見ないので、これを実装してみます。参考とした論文は(Jones&Pewsey, 2012)と、Pewseyらの書いた"Circular statistics in R"です。

Circular Statistics in R

Circular Statistics in R

結果

例によってpythonです。Rの本を見てるのに…。　

逆変換で知りたい値は既知の t, \mu, \kappa, \nuのもとで t = \theta -\mu - \nu(1+\cos(\theta - \mu))を満たすような \thetaです。観測値= tが既知ということがポイントです。この場合には g(\theta) = -t + \theta -\mu - \nu(1+\cos(\theta - \mu))という関数を考えて、 g(\theta) = 0となるような \thetaを求めます。どちらにせよ非線形な問題ですが、0となる値を求めるには効率的なアルゴリズムがあるので、それを利用することができます(Wikipediaにもそんな記載があります)。3つの手法を紹介します。

シミュレーションデータは次のように作成しました。歪度パラメータが0である場合、通常のvon Mises分布と一致しますので、きちんと0が推定されるか調べます。

I = 1000
RADIAN = vonmises.rvs(size=I, loc=0, kappa=1.0)
stan_data = {
    "I": I,
    "RADIAN": RADIAN
}

Stanの組み込み関数を利用する

StanのVersion 2.17.0以降には、algebra_solverという関数で、非線形方程式の場合にも解を得ることができます。この関数はPowell法を使っています(Powell, 1970)。Stanコードの実装は次のとおりです。

  • 1~17, 48行目: 逆変換をする処理です。
  • 24~33行目: algebra_solverへ投入するデータを宣言しています。

algebra_solverはStanのマニュアルの20節に記述があります。第1引数へ解を求める関数、第2引数へその際の解、第3引数へパラメータ、第4引数へ実数型の定数値、第5引数へ整数型の定数値を使います。ちょっと使い方にはコツがあります。

  • 先程も書きましたが、今回の場合は観測値= tが既知ということがポイントです。これがパラメータになりますので、第3引数へ入れます。
  • その他モデル上でのパラメータ \mu, \nuなどもパラメータです。普通のプログラミング言語ではkargsなんかを使うのですが、第3引数にはvector型しか受け付けないので、観測値の長さより少し伸ばして代入します。
  • 定数値は今回の場合、観測値の長さしかありません。これは整数型です。実数型に該当するものは無いのですが、宣言は必要なので長さ0のベクターをtransformed_dataのブロックで宣言しておきます。

性能評価してみましょう。サンプルサイズを変えてデータを何回か生成し、真の分布に対するKL divergenceを調べます。

result = []
for I in [100, 300, 500, 1000]:
    for i in range(5):
        RADIAN = vonmises.rvs(size=I, loc=0, kappa=1.0)
        stan_data = {
            "I": I,
            "RADIAN": RADIAN
        }

        fit = model.optimizing(stan_data, init_alpha=1e-10)
        p = invBvonmises_pdf(theta, kappa=fit["kappa"], nu=fit["nu"], loc=fit["mu"])
        pt = invBvonmises_pdf(theta, kappa=1.0, nu=0, loc=0)
        kld = entropy(p, pt)
        tmp = {"I": I, "i": i, "kld": kld}
        result.append(tmp)
df = pd.DataFrame(result)

fig = plt.figure()
ax = fig.add_subplot(111)
sns.boxplot(data=df, x="I", y="kld", ax=ax)
ax.set_xlabel("Sample size")

f:id:ajhjhaf:20181126092909p:plain

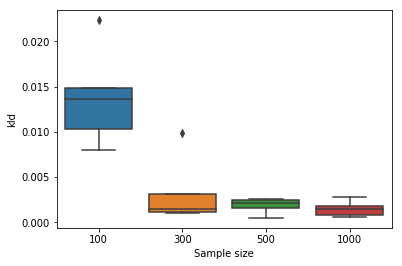
データ量に応じてきちんと真の分布との距離が小さくなっていることがわかります。

ニュートン法

組み込み関数は目的関数だけあれば使える便利な手法ですが、めちゃめちゃ遅いです。ベクトル形式で渡していますが、データ数がある程度あるとほとんど使い物になりません。I=500の時点で、平均11秒ほどかかります。今回の実験がMCMCではなく、MAP推定で実行しているのもそれが理由となります。幸いにも、今回の変換は微分可能な形式で示されていますので、傾きの情報を利用したニュートン法が一つのアイディアとして考えられます。この場合には解が二次収束しますので、非常に早く計算可能です。Stanのコードは次のとおりです。

  • 1~23, 38行目: ニュートン法での逆変換です。
    • 8行目: 初期値として、 \thetaの値を使います。色々試したが、この関数の場合はこれが安定的でした。
    • 9行目: g(\theta)を評価します。これがすべて0なら理想形です。
    • 10行目: 絶対値を取って、どれだけ0に近付ているか評価します。
    • 11行目: 反復回数の上限値を決めます。これを決めておかないと、何かあって0に近づかなかった場合は無限に計算されてしまいます。
    • 12行目: どれだけ0に近づいたら終了するか決めます。Stanの場合はmachine_precision()が計算機イプシロンとして用意されていますので、これを使います。
    • 13~15行目: tを傾きを使って更新して、誤差を再評価します。12行目で決めた基準より小さくなったら終了です。
    • 16~19行目: 反復回数が上限に達したら、反復を強制的に終了します。

先ほどと同様の誤差計算は次のとおりになります。こちらでも、問題なくKL divergenceが0に近づいています。

f:id:ajhjhaf:20181126094621p:plain

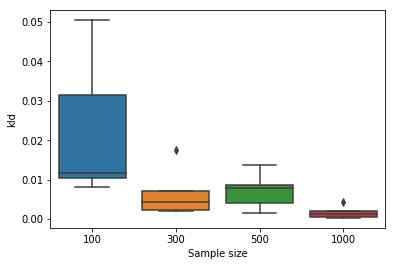
肝心の速度についてもI=500の段階で0.1秒と100倍ほど高速化することができました。2つの手法を比較すると、次のとおりになります。Powellが指数増加していることがわかります。

f:id:ajhjhaf:20181126094802p:plain

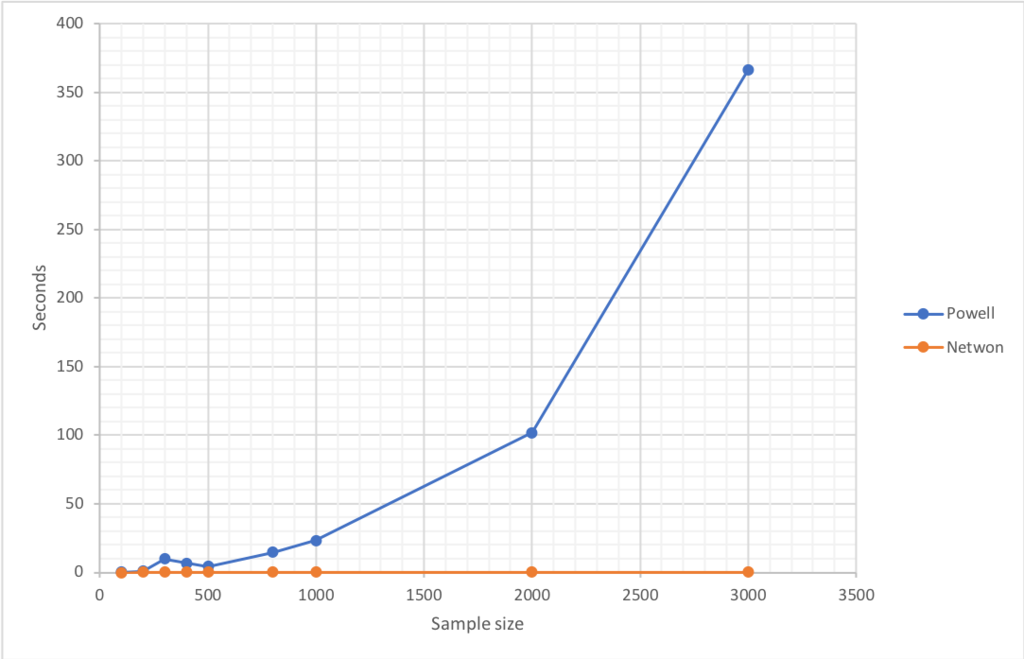
二分法

ニュートン法でハッピーエンドを迎えられるかと思いきや、そうはなりません。RstanにはStanの関数を呼び出すexpose機能があります。 s(t)がどのような挙動をするか調べてみましょう。先程のモデルを適当に保存してください。

library("rstan")
rstan::expose_stan_functions("Desktop/invBvonmises.stan")
x = seq(-pi, pi, length=1000)
mu = 0
nu = 0.99
I = 1000
y = inv_transformation_Batschelet(x, mu, nu, I)
plot(x, y)

f:id:ajhjhaf:20181126095608p:plain

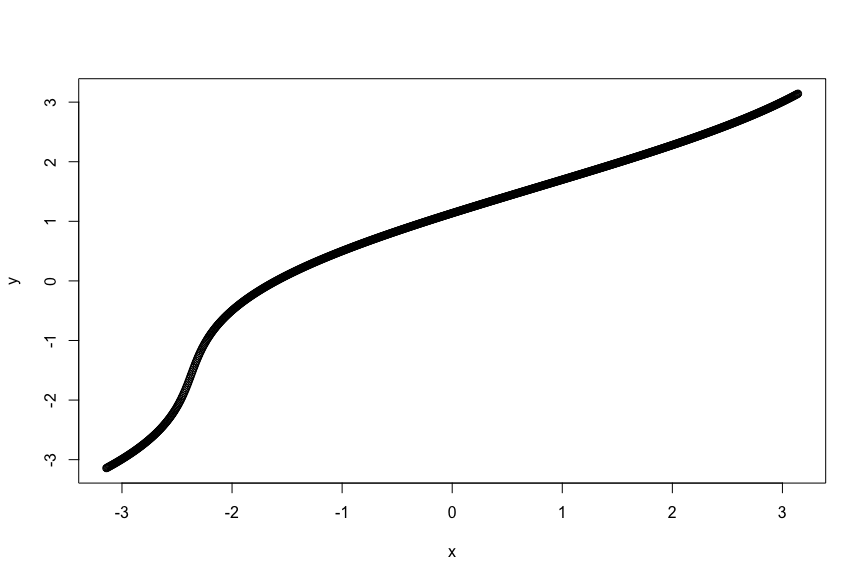
良さそうに見えます。が、ここでnuの値を極めて大きくしてみましょう。

f:id:ajhjhaf:20181126095532p:plain

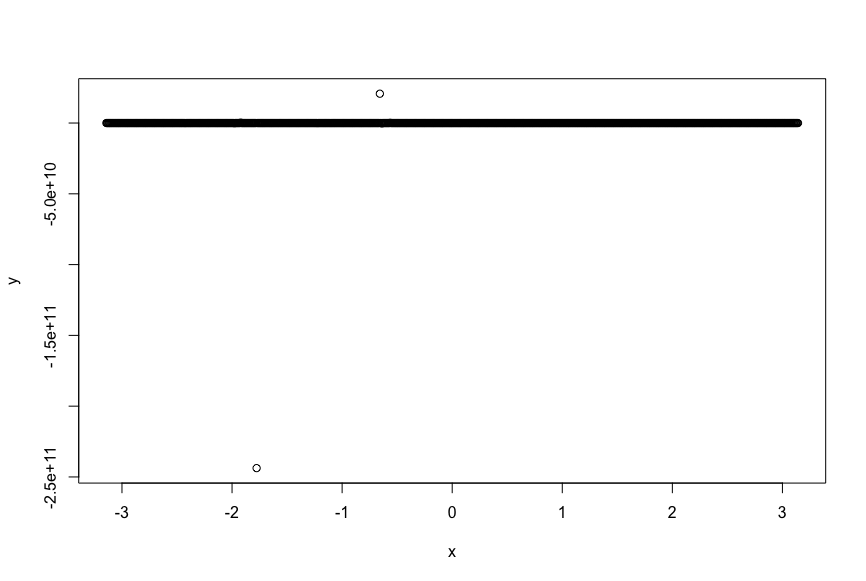
ぶっ壊れた値が出てきてしまいました。これは、 \nuが大きい場合に、勾配が消失することが原因と思われます。 g(\theta)を \nuが大きい場合に書いてみますと、次のとおりです。

mu = 0
nu = 0.99
theta = 0
x = np.linspace(-np.pi, np.pi, 1000)
y = x - nu * (1 + np.cos(x - mu)) - theta

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y)
ax.set_xlabel("theta")
ax.set_ylabel("g(theta)")

f:id:ajhjhaf:20181126095943p:plain

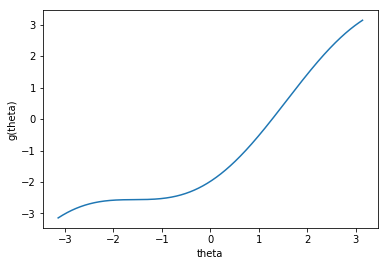
thetaが-2から-1の場合にかけて、勾配が消失していることが見て取れます。この場合には、傾きを使わない手法として、二分法を使うことが考えられます。Stanのモデルは次のとおりです。

  • 1~34行目: 二分法による逆変換です。
    • 10-11行目: 上界、下界を決めます。求める解の範囲が -\piから \piなので、それぞれ g(\theta)が0以上、以下となるように決めましょう。
    • 12行目: 上界、下界から真ん中の値をとります。
    • 13-14行目: ニュートン法と同様に、 g(\theta)の評価をして、誤差を調べます。
    • 17-23行目: 評価値の正負に応じて、上界、下界を狭めます。pythonだったらnumpyのsmart indexを使えば一行でかけますが、Stanだとfor文で一つ一つ判定しなくてはいけません
    • 28行目: 二分法は一次収束です。ニュートン法と同等の精度を得るために、1000(>302)回を反復上限とします。

R側から呼び出して、同様に計算させてみると、変換できたことがわかります。

f:id:ajhjhaf:20181126104135p:plain

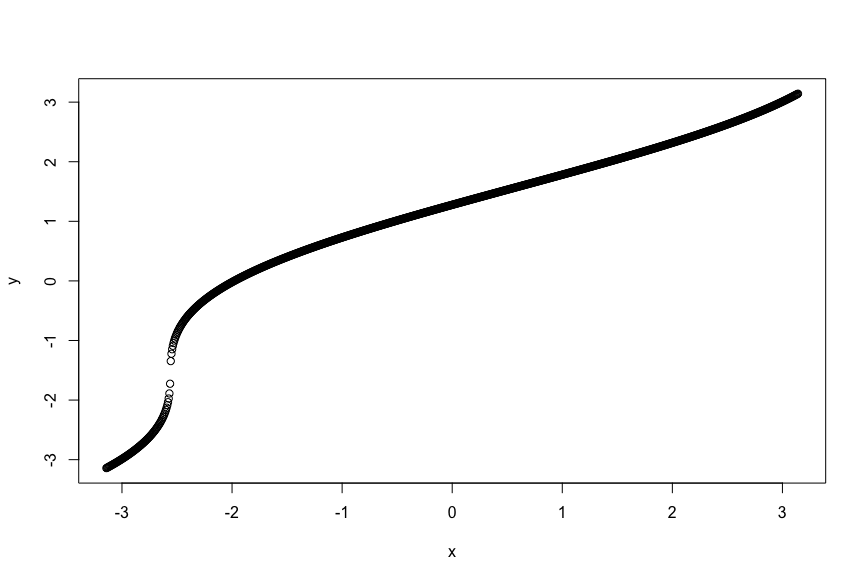
が、ここで大きな問題があります。R側での動作を見るに動きそうなこのモデルですが、実際に動かしてみるとLS failedが発生してうまくいきません。ナンデ……。大きな \nuから作ったデータに対してフィッティングしてエラーが起こるなら、変換の勾配が消失して微分できず失敗すると納得できるのですが、ここまで使ってきた \nu=0のデータに対して実行してもやはり失敗します。

まとめ

陽的に式をかけない変換を含むモデリングを実行することができました。Powell法だと(おそらく)数値的に安定なので使いやすいですが、データが多い場合には変換が非効率でめちゃめちゃ時間がかかります。ニュートン法は超絶早いですが、傾きがある場合じゃないと使えません。手元でまともに動く範囲を調べて、パラメータ制約つけるのがいいでしょうか…。二分法はなぜかうまくいきません。困った(ちなみにdiscourseで絶賛助けを求めています、コメント歓迎です……)。

今回利用したコードは、こちらにあります。再現実験したい方はどうぞ。

謝辞

このブログ記事を書くにあたり、StanのdiscourseでBen Bales氏に助けていただきました。お礼を申し上げます。

StanのThreading動作確認

ベイジアンモデリング

TL; DR

導入

PyStanは2.18.0系からStanに搭載されたThreading機能を使うことができるようになりました。公式のドキュメントはこちらになります*1。

この機能は、今までのMCMC chainごとにスレッドをフォークして並列化するのではなく、MCMCサンプル内での並列化です。先程のリンク先のExampleの欄にも書かれているとおりに、chain数×設定スレッド数分の並列化ができるように成りました。ただし、まだかなり作りかけの機能であるため、運用上は幾つか疑問点があります。

  • 並列化することでどれほど早くなるのか？
  • 単一のMCMC chainの場合でも並列化されるのか？
  • 並列化したことで推論結果が悪くなることはあるのか？
  • 設定スレッドはモデルのコンパイル時のみ影響するのか？サンプリング時にも影響するのか？

以上の疑問を解決するために、モデルを実際に動かしてみました。

手法

環境

次のとおりです。

  • pystan 2.18.0
  • python 3.6.5
  • CPU数 32
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
from scipy.stats import norm
from pystan import StanModel
import pystan

print(pystan.__version__)
print(os.cpu_count())

モデル

Exampleに記載されているeight-school problemのデータとモデルをそのまま利用します。

model_code = """
functions {
  vector bl_glm(vector mu_sigma, vector beta,
                real[] x, int[] y) {
    vector[2] mu = mu_sigma[1:2];
    vector[2] sigma = mu_sigma[3:4];
    real lp = normal_lpdf(beta | mu, sigma);
    real ll = bernoulli_logit_lpmf(y | beta[1] + beta[2] * to_vector(x));
    return [lp + ll]';
  }
}
data {
  int<lower = 0> K;
  int<lower = 0> N;
  vector[N] x;
  int<lower = 0, upper = 1> y[N];
}
transformed data {
  int<lower = 0> J = N / K;
  real x_r[K, J];
  int<lower = 0, upper = 1> x_i[K, J];
  {
    int pos = 1;
    for (k in 1:K) {
      int end = pos + J - 1;
      x_r[k] = to_array_1d(x[pos:end]);
      x_i[k] = y[pos:end];
      pos += J;
    }
  }
}
parameters {
  vector[2] beta[K];
  vector[2] mu;
  vector<lower=0>[2] sigma;
}
model {
  mu ~ normal(0, 2);
  sigma ~ normal(0, 2);
  target += sum(map_rect(bl_glm, append_row(mu, sigma),
                         beta, x_r, x_i));
}
"""

stan_data = dict(
    K = 4,
    N = 12,
    x = [1.204, -0.573, -1.35, -1.157,
         -1.29, 0.515, 1.496, 0.918,
         0.517, 1.092, -0.485, -2.157],
    y = [1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1]
)

パラメータ

モデルは次の4つをコンパイルしました。

  • extra_args等の一切を無指定(以下Vanillaと呼称)
  • extra_argsを指定 + STAN_NUM_THREADS=1と指定(THREADS1と呼称)
  • extra_argsを指定 + STAN_NUM_THREADS=4と指定(THREADS4と呼称)
  • extra_argsを指定 + STAN_NUM_THREADS=8と指定(THREADS8と呼称)

これとは別に以下のパラメータをサンプリング時に指定しました。

  • サンプリング直前にSTAN_NUM_THREADSを再設定
  • n_jobs(公式APIでは"Sample in parallel. If -1 all CPUs are used. If 1, no parallel computing code is used at all, which is useful for debugging."と書かれているが、これがThreadingに影響するのか、MCMC chainだけに影響するのか不透明)
  • iter(MCMCの反復数)
  • chains(MCMCのchain数)

実験

上述のパラメータを設定した上で、jupyter labの%timeitオプションを付けて実行しました。各パラメータセットごとに7回反復されて、平均が取られました。notebookはこちらです。

結果

index compile num_threads sampling num_threads n_jobs iter chains avarage time std time
1 Vanilla 1 4 2000 2 0.883 0.121
2 Vanilla 1 2 2000 2 0.834 0.0624
3 Vanilla 1 4 2000 2 0.935 0.181
4 Vanilla 1 1 2000 2 1.21 0.413
5 Vanilla 1 1 2000 1 0.554 0.0567
6 Vanilla 1 1 20000 1 4.36 0.296
7 Vanilla 1 8 2000 2 0.82 0.0896
8 1 1 4 2000 2 0.936 0.0743
9 1 1 2 2000 2 0.967 0.101
10 1 1 4 2000 2 0.937 0.0693
11 1 1 1 2000 2 1.27 0.0501
12 1 1 1 2000 1 0.678 0.0833
13 1 1 1 20000 1 5.34 0.804
14 1 1 8 2000 2 0.962 0.0777
15 4 4 4 2000 2 3.63 0.547
16 4 4 2 2000 2 3.54 0.434
17 4 1 4 2000 2 0.99 0.0883
18 4 4 1 2000 2 5.4 0.576
19 4 4 1 2000 1 2.68 0.216
20 4 4 1 20000 1 21.1 1.11
21 4 4 8 2000 2 3.27 0.274
22 8 8 4 2000 2 3.28 0.456
23 8 8 2 2000 2 3.43 0.263
24 8 1 4 2000 2 0.865 0.13
25 8 8 1 2000 2 4.91 0.434
26 8 8 1 2000 1 2.52 0.314
27 8 8 1 20000 1 22.8 4.12
28 8 8 8 2000 2 3.31 0.341

average timeとstd timeの単位は秒です。

  • VanillaはSTAN_NUM_THREADSが1の場合と殆ど変わりません。中途処理があるからか、0.1秒ほど遅くなっています(Compare 1, 2, 7... vs 8, 9, ..., 14)。

  • n_jobsはchain数より大きい値を入れても早くなりません(Compare 15 vs 16等)。

    • 一方で、chain数より小さな値を入れれば、並列でMCMCできなくなるので遅くなります(Compare 15 vs 18等)。
    • また、STAN_NUM_THREADSのパフォーマンスにも影響しないようです(Compare 22 vs 23)。

  • 環境変数に設定したSTAN_NUM_THREADSは、サンプリング時にも影響するようです(Compare 15 vs 17等)。

    • コンパイル時の値は上限スレッド数というだけで、実効値は環境変数を参照するのでしょう。
    • 即ち、SGEなどのqueuing systemを使っているときには、サンプリング時に環境変数をセットする必要があります。

  • 推論結果は、見た感じ悪化しませんでした(実行結果を参照)。

  • 一番大事なことですが、 Threadingをしても遅くなるだけです (Comapare 2 vs 9 vs 16 vs 23)。

    • モデルが単純でデータが少ないからでしょうか？iter数を増やしてみればThreadingの恩恵があるかと思いましたが、傾向は変わりませんでした(Compare 6 vs 13 vs 20 vs 27)。
    • ぜひどなたかに、複雑なモデルで実験してほしいです(自分には適当なものが思いつきませんでした)。
    • %timeitがマルチスレッドの場合は時間×スレッド数をはじき出すかと思い、timeモジュール+自分の時間間隔でも計測しましたが、やはり遅かったです。

  • サンプリング時にhtopコマンドでCPU利用数を見ていましたが、高々200%ぐらいになるだけで、本来理想としていた800%等になることはありませんでした。

追記(2018-10-10)

@nan_makersstat さんや id:StatModeling (@hankagosa)さんから次のような指摘をいただきました。

というわけで、軽く実験してみます。モデルは簡単な一次回帰です。シミュレーション的にデータを10万点作成します。 注: 以下のモデルはThreadingで必要なmap_rect関数が使われていないので早くなるはずはありません。map_rect用のモデルは後述しました(2018-10-19)

model_code = """
  data {
    int I ;
    real x[I] ;
    real y[I] ;
  }
  
  parameters {
    real a ;
    real b ;
  }
  
  model {
    for (i in 1:I){
      y[i] ~ normal(a * x[i], b) ;
    }
  }
  
  generated quantities {
    real log_likelihood[I] ;
    for (i in 1:I){
      log_likelihood[i] = normal_lpdf(y[i] | a * x[i], b) ;
    }
  }
"""

I = 100000
a = 1
b = 1
x = np.linspace(-1, 1, I)
y = norm.rvs(loc=a*x, scale=b)

stan_data = {
    "I": I,
    "x": x,
    "y": y
}

これをVanilla, STAN_NUM_THREADS=1, STAN_NUM_THREADS=4で投入してみました。計測方法は同じで7回の平均です。

index compile num_threads sampling num_threads n_jobs iter chains avarage time std time
1 Vanilla 1 2 100000 2 111 5.5
2 1 1 2 100000 2 113 5.65
3 4 4 2 100000 2 108 5.71

うーん、ちょっとだけ早くなっています。しかしt検定で有意差が出る気がしません。おそらくデータ数を増やせばより効果があるのではないでしょうか。 何れにせよ、小標本なのにThreadingが必要なほどサンプリングで時間がかかりすぎている場合は、モデルが適切でない可能性をまず考えるべきです。丁寧に、メカニズムを考えて、モデルを改良していきましょう！

追記(2018-10-18)

discourseで質問したところ、ThreadingやMPIのような操作をするためには、データやモデルをそれ専用に作り変える必要があるとの回答を頂きました。 まだ試せていませんが、cmdstanを使った例についてはこのリポジトリが参考になります。ご参考までに。

追記(2018-10-19)

map_rect用のモデルを別に書いて実験しました。ついでにデータ数は合成に100万まで増やしてみました。実験につかったnotebookはこちらです。

index compile num_threads sampling num_threads n_jobs iter chains avarage time std time
1 Vanilla 1 1 500 1 128 6.71
2 4 4 4 500 1 173 5.71

なんと、やっぱり遅くなってしまいました。しかし、やはりtop等のコマンドで確認してもCPU使用率が100%までいかないんですよね。別の原因がある気がしますが、現状不明です。

*1:この機能は単体のマシンでの並列化であり、MPI 環境を使った並列化はまた別に実装されています

離散ハート型分布の導出とシミュレーション

解析

概要

相変わらず、ちょこちょこと円周統計を勉強しています。

角度データのモデリング ＩＳＭシリーズ：進化する統計数理

角度データのモデリング ＩＳＭシリーズ：進化する統計数理

テキスト中では、方向統計の分布としてハート型分布が紹介されています。この分布は

f(\theta) = \frac{1 + 2\rho\cos{(\theta)}}{2\pi}

の確率密度関数を持つ分布です。確率密度関数や、そこからサンプリングした乱数を可視化すると次のようになります。左側の図がユークリッド空間、右側の図が極座標系です。

f:id:ajhjhaf:20180724124401p:plain

他にも円周分布として、有名なvon Mises分布、巻き込みコーシー分布、巻き込み正規分布、一般化ハート型分布(or Jones-Pewsey分布)などなども書かれています。

以上に挙げた分布は全て連続分布です。テキスト中では一節割かれて、格子分布が紹介されていますが詳しくありません。しかし実際に角度のデータが観測された場合には、有限個の離散値になることが多いのではないでしょうか。この記事ではハート型分布を離散化することで、分布を導出し、乱数生成もしてみます。

分布の導出

先程も書いたハート型分布を変形させて、離散化させてみます。アプローチとしては単純で、確率分布 f(\theta)に対して、

\int_{\theta-\alpha}^{\theta+\alpha} f(\theta) d\theta

を計算します。円周全体が L個に分割されているとしたら、それぞれの \alphaは前後の角度との差分になるので、 \alpha = \frac{2\pi}{2L} = \frac{\pi}{L}で求まります。というわけで、以上の結果をSympyで計算してみます。

import sympy
init_printing(use_unicode=True)
from sympy import symbols, integrate, simplify, init_printing, cos, pi
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'

theta, mu, rho, Theta, alpha = symbols("theta, mu, rho, Theta, alpha", real=True)
c_pdf = (1 + 2 * rho * cos(theta - mu)) / (2 * pi)
c_pdf_int = integrate(c_pdf, (theta, Theta-alpha, Theta + alpha))
simplify(c_pdf_int)

結果は \frac{1}{\pi} \left(\alpha + 2 \rho \sin{\left (\alpha \right )} \cos{\left (\Theta - \mu \right )}\right) = \frac{1}{\pi} \left(\frac{\pi}{L} + 2 \rho \sin{\left (\frac{\pi}{L} \right )} \cos{\left (\Theta - \mu \right )}\right)

として得られます。とりあえず適当に、離散ハート型分布などと名付けます*1。

乱数の生成

どのような挙動をするか興味がありますので、この分布に従った乱数を生成してみます。乱数生成についても上述したテキストに書いてあります。よく使われるのは逆関数法ですが、ハート型分布では逆関数の導出が難しいので現実的ではないそうです。離散ハート型分布も同じでしょう。ここでは並べて紹介されている棄却採択法(棄却サンプリング)を使います。といっても、テキストで紹介されていた棄却採択法は連続分布に対するものだったので、MathWorksの記事を参考にしました。手順は殆ど変わらず、乱数を作りたい分布 P_p(\Theta)に対して

  1. 任意の分布 P_q(\Theta)を選ぶ
  2. P_pと P_qからサンプリングされる任意の値 p_i, q_iに対して、 \frac{p_i}{q_i} \leq cを満たすようなcをとる
  3. [0, 1]の一様乱数から乱数 uを生成する
  4. P_qから乱数 vを生成する
  5. u \leq \frac{P_p(v)}{cP_q(v)}を満たすようなら乱数として採択、満たさないなら棄却する
  6. 3に戻る

を繰り返すだけです。

テキストでは連続分布であったため、 P_qとして \frac{1}{2\pi}を使っていましたが、この問題では離散分布であるので、 \frac{1}{L}を使います。このときに

\frac{1}{\pi} \left(\frac{\pi}{L} + 2 \rho \sin{\left (\frac{\pi}{L} \right )} \cos{\left (\Theta - \mu \right )}\right) \leq \frac{c}{L}を満たすようなcの最小値は

c = 1 + \frac{2L}{\pi}\rho\sin{(\frac{\pi}{L})}

となります。単純に不等式を解くだけです。これを実装してみると次のようになりました。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from collections import Counter
from scipy.stats import randint

def polar_twin(ax):
    ax2 = ax.figure.add_axes(ax.get_position(),
                             projection='polar',
                             label='twin',
                             frameon=False,
                             theta_direction=ax.get_theta_direction(),
                             theta_offset=ax.get_theta_offset())
    ax2.xaxis.set_visible(False)

    for label in ax.get_yticklabels():
        ax.figure.texts.append(label)

    return ax2

def dcardioid_pmf(theta, loc, rho, L):
    pmf = (np.pi / L + 2 * rho * np.sin(np.pi / L) * np.cos(theta - loc)) / np.pi
    return pmf

# AR法での実装
def dcardioid_rvs(rho, loc, size, L):
    c = 1 + 2 * L * rho * np.sin(np.pi / L) / np.pi
    result = []
    while len(result) != size:
        u = np.random.uniform(0.0, 1.0)
        v = randint.rvs(0, L) * 2 * np.pi / L
        p = dcardioid_pmf(v, rho=rho, loc=loc, L=L)
        q = 1 / L
        if u < p / (c * q):
            result.append(v)
    return result

# 乱数の長さ
I = 5000
# 区分する数(L)
num_r = 360
#分布のパラメータ
mu = 0
rho = 0.45

# 範囲
r = np.arange(0, 2 * np.pi, 2 * np.pi / num_r)
# 確率密度関数の取得
f1 = dcardioid_pmf(r, loc=mu, rho=rho, L=num_r)
# 乱数生成
y = dcardioid_rvs(rho=rho, size=I, loc=mu, L=num_r)
# 乱数をgroupingして数え上げる
c = Counter(y)
ydf = pd.DataFrame(list(c.items()), columns = ["theta", "count"])
ydf = pd.DataFrame(np.arange(0, num_r, 1) * 2 * np.pi / num_r, columns = ["theta"]).merge(ydf, how="outer", on=["theta"])
y_hist = ydf["count"]
width = 2 * np.pi / num_r


# 可視化
fig = plt.figure(figsize=(10,5))

# ユークリッド系
ax = fig.add_subplot(1,2,1)
ax.plot(r, f1)
ax2 = ax.twinx()
ax2.plot(r, y_hist)

# 極座標系
ax = fig.add_subplot(1,2,2, projection="polar")
ax.plot(r, f1)
ax.set_theta_zero_location("N")
ax.set_rticks(np.linspace(0, round(ax.get_rmax()+0.05, 1), 3))
ax2 = polar_twin(ax)
ax2.bar(r, y_hist, width=width*0.90)
ax2.set_theta_zero_location("N")
ax2.set_rticks(np.linspace(0, round(ax2.get_rmax(), 0), 3))
ax2.set_rlabel_position(ax.get_rlabel_position() + 180)
  • 極座標系で二軸プロットをするためには、以下のQ&Aを参考に改造しました。
    • 最新版のmatplotlibにはラベルを指定するメソッドが追加されているので、polar_twinの中でラベルの角度を指定する必要がありません。

stackoverflow.com

  • 離散角度の数え上げはcounter + pandasでjoinという超まどろっこしいことをしています。もっと美しいコードはあるはずです。

    • np.histogramでやってみたのですが、境界値の選択が雑なのか、上手くいきませんでした。

  • 棄却採択法での乱数生成ももっと綺麗に書けますが、上述した解説と対応させました。

結果は次のとおりになります。シミュレーション結果も上々です。

f:id:ajhjhaf:20180724125649p:plain

他の分布でも使えるか？

今回はハート型分布を離散化することが出来ましたが、この手順による拡張は他の分布にも使うことが出来るでしょうか？個人的には結構難しいと思います。

巻き込みコーシー分布を考えます。同じように積分すると、

\begin{cases} - \frac{1}{4 \pi} \left(\rho^{2} - 1\right) \left(\tan{\left (- \frac{\Theta}{2} + \frac{\alpha}{2} + \frac{\mu}{2} \right )} + \tan{\left (\frac{\Theta}{2} + \frac{\alpha}{2} - \frac{\mu}{2} \right )}\right) & \text{for}\: \rho = -1 \\\frac{1}{4 \pi} \left(\rho^{2} - 1\right) \left(\frac{1}{\tan{\left (\frac{\Theta}{2} + \frac{\alpha}{2} - \frac{\mu}{2} \right )}} + \frac{1}{\tan{\left (- \frac{\Theta}{2} + \frac{\alpha}{2} + \frac{\mu}{2} \right )}}\right) & \text{for}\: \rho = 1 \\\frac{i}{2 \pi} \left(\log{\left (\frac{1}{\rho + 1} \left(- i \rho + \left(\rho + 1\right) \tan{\left (- \frac{\Theta}{2} + \frac{\alpha}{2} + \frac{\mu}{2} \right )} + i\right) \right )} - \log{\left (\frac{1}{\rho + 1} \left(- i \rho - \left(\rho + 1\right) \tan{\left (\frac{\Theta}{2} + \frac{\alpha}{2} - \frac{\mu}{2} \right )} + i\right) \right )} - \log{\left (\frac{1}{\rho + 1} \left(i \rho + \left(\rho + 1\right) \tan{\left (- \frac{\Theta}{2} + \frac{\alpha}{2} + \frac{\mu}{2} \right )} - i\right) \right )} + \log{\left (\frac{1}{\rho + 1} \left(i \rho - \left(\rho + 1\right) \tan{\left (\frac{\Theta}{2} + \frac{\alpha}{2} - \frac{\mu}{2} \right )} - i\right) \right )}\right) & \text{otherwise} \end{cases}

が得られました。わお。これを使うのはしんどいでしょ。

von Mises分布では

\frac{1}{2 \pi I_{0}\left(\rho\right)} \int_{\Theta - \alpha}^{\Theta + \alpha} e^{\rho \cos{\left (\mu - \theta \right )}} d\theta

が得られます。この積分は陽に解析解が出ないようです。

積分する方法以外に、各分布の分布関数を \alphaだけ変化させたときの差分を確率密度関数として使うことも考えましたが、巻き込みコーシーもvonMisesでも式が綺麗にならなかったので諦めました*2。連続的に便利な分布でも、簡単に離散化できないんだなぁ、といういい勉強になりました。

*1:discrete cardioid distributionで調べると一件だけ統計数理研究所のセミナーがヒットしますが、他に資料がありません。参考にしたいなぁ。。

*2:というか、von Mises分布は恒等関数や無限和が入ってきて扱いづらい